高中物理2021年初专题周练——运动的合成与分解训练题（一）【含详解】
高中
整体难度：中等
2021-01-13
题号
一
二
三
四
五
评分
一、选择题 (共86题)
添加该题型下试题
1.
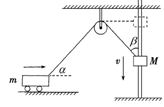
如图所示，重物M沿竖直杆下滑，并通过一根不可伸长的细绳带动小车沿水平面向右运动．若当滑轮右侧的绳与竖直方向成
角，且重物下滑的速率为v时，滑轮左侧的绳与水平方向成
角，则小车的速度为 ( )
A．
B．
C．
D．
难度：
知识点：运动的合成与分解
使用次数：135
【答案】
D
【详解】
将速度v按运动效果分解如图所示：
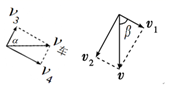
则沿绳方向v1＝vcos
，同理分解小车速度，
，因为绳不可伸长，故沿绳方向速度大小相等. 
,所以
cos
,所以
；故选D.
【点睛】
本题通常称为绳端物体速度分解问题，一定注意合运动是物体的实际运动．
2.
如图所示，汽车用跨过定滑轮的轻绳提升物块A．汽车匀速向右运动，在物块A到达滑轮之前，关于物块A，下列说法正确的是
A．将竖直向上做匀速运动
B．将处于失重状态
C．将处于超重状态
D．将竖直向上先加速后减速
难度：
知识点：运动的合成与分解
使用次数：140
【答案】
C
【详解】
设绳子与水平方向的夹角为θ，将小车的速度分解为沿绳子方向和垂直于绳子方向，沿绳子方向的速度等于A的速度，根据平行四边形定则得vA=vcosθ，车子在匀速向右的运动过程中，绳子与水平方向的夹角为θ减小，所以A的速度增大，A做加速上升运动，且拉力大于重物的重力，A处于超重状态，故ABD错误，C正确．
【点睛】
解决本题的关键会对小车的速度进行分解，知道小车的速度是沿绳子方向和垂直于绳子方向速度的合速度．
3.
如图所示，重物M沿竖直杆下滑，并通过绳子带动小车m沿斜面升高。则当滑轮右侧的绳子与竖直方向成θ角且重物下滑的速度为v时，小车的速度为
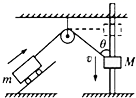
A．vcosθ B．vsinθ C．
D．vtanθ
难度：
知识点：运动的合成与分解
使用次数：133
【答案】
A
【解析】
物体M以速度v沿竖直杆匀速下滑，绳子的速率等于小车m的速率，将M物体的速度分解为沿绳子方向和垂直于绳子方向，沿绳子方向的分速度等于绳速，由几何知识求解m的速率，从而即可求解.
【详解】
将M物体的速度按图示两个方向分解，如图所示：
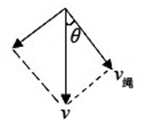
得绳子速率为
，而绳子速率等于小车m的速率，则有小车m的速率为
；故A正确
【点睛】
本题通常称为绳端物体速度分解问题，容易得出的结果是将绳的速度分解，一定注意合运动是物体的实际运动,是把合速度分解成两等效的分速度.
4.
根据高中所学知识可知，做自由落体运动的小球，将落在正下方位置．但实际上，赤道上方200m处无初速下落的小球将落在正下方位置偏东约6cm处，这一现象可解释为，除重力外，由于地球自转，下落过程小球还受到一个水平向东的“力”，该“力”与竖直方向的速度大小成正比，现将小球从赤道地面竖直上抛，考虑对称性，上升过程该“力”水平向西，则小球
A．到最高点时，水平方向的加速度和速度均为零
B．到最高点时，水平方向的加速度和速度均不为零
C．落地点在抛出点东侧
D．落地点在抛出点西侧
难度：
知识点：运动的合成与分解
使用次数：227
【答案】
D
【解析】
AB、上升过程水平方向向西加速，在最高点竖直方向上速度为零，水平方向上有向西的水平速度，且有竖直向下的加速度，故AB错；
CD、下降过程向西减速，按照对称性落至地面时水平速度为0，整个过程都在向西运动，所以落点在抛出点的西侧，故C错，D正确；
故选D
点睛：本题的运动可以分解为竖直方向上的匀变速和水平方向上的变加速运动，利用运动的合成与分解来求解．
5.
在光滑的水平面上，一质量为m =2kg的滑块在水平方向恒力F=4 N的作用下运动．如图所示给出了滑块在水平面上运动的一段轨迹，滑块过P、Q两点时速度大小均为
,滑块在P点的速度方向与PQ连线夹角
， 
，则下列说法正确的是（ ）
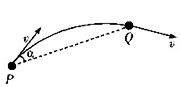
A．水平恒力F的方向与PQ连线成53°夹角
B．滑块从P点运动到Q点的时间为3s
C．滑块从P点运动到Q点的过程中速度最小值为3 m/s
D．P、Q两点连线的距离为10 m
难度：
知识点：运动的合成与分解
使用次数：195
【答案】
B
【解析】
A、滑块在水平恒力作用下由P到Q，滑块过P、Q两点时速度大小均为
，即水平恒力不做功，所以力应该和位移的方向垂直，A错；
B、把速度分解到垂直于PQ方向上则：
在这个方向上滑块先减速后反向加速，运动的加速度
运动具有对称性，得
B对；
C、把速度分解到PQ方向
，做匀速运动．所以当滑块在垂直于PQ方向上的速度等于零时，此时运动的速度最小，最小为4m/s故C错；
D、PQ两点之间的距离为：
，故D错；
综上所述本题答案是：B
本卷还有95题，登录并加入会员即可免费使用哦～
立即下载
全选试题
编辑试卷
收藏试卷
试题总数：
100
总体难度：
中等
难度统计
难度系数
数量
占比
偏难
26
26.0%
中等
46
46.0%
容易
21
21.0%
基础
5
5.0%
很难
2
2.0%
题型统计
大题类型
数量
占比
选择题
86
86.0%
解答题
14
14.00%
知识点统计
知识点
数量
占比
运动的合成与分解
92
92.0%
实验：探究平抛运动的特点
1
1.0%
共点力的平衡
1
1.0%
牛顿第二定律
3
3.0%
能量守恒定律
1
1.0%
牛顿运动定律的应用
1
1.0%
匀变速直线运动的速度与时间的关系
1
1.0%
版权提示
该作品由: 用户王然分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益，请联系 可圈可点 ，我们核实后将及时进行处理。