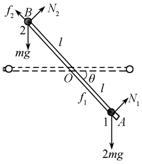
如图，刚性细轻杆（其质量可视为零）可绕通过其中的点的光滑水平轴在竖直面内自由转动。两质量分别为和的小球1和2（可视为质点）串在轻杆上，它们与轻杆之间的静摩擦系数为。开始时轻杆静止在水平位置，小球1和2分别位于紧靠轻杆两端和的位置。现让系统自水平位置以零初速下摆，求

1．小球1脱离轻杆时的位置（用小球1脱离杆时杆与水平线的夹角表示）；

2．小球2脱离轻杆时的位置（用小球2脱离杆时杆与水平线的夹角表示）。

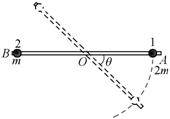
答案

设轻杆的杆长为，当杆与水平线的夹角为时，球1和球2的速度分别为和，杆转动的角速度为。因机械能守恒，有

。                （1）

又因

，                                                                      （2）

可由（1）、（2）解得

                                                               （3）

轻杆与两小球构成的系统对转轴的角动量

，                                                               （4）

由角动量定律有

。                                        （5）

根据角加速度的定义

，                                                                    （6）

由（2）、（4）、（5）、（6）各式得

。                                                                      （7）

当两球都未脱离轻杆时，两球都绕转轴作圆周运动，球1的切向加速度和法向加速度分别为

                                                                        （8）

                                                                        （9）

以表示沿垂直于轻杆方向球1与杆的相互作用力的大小，以表示沿着轻杆方向球1与杆的相互作用力的大小，根据牛顿第二定律，有

，                                                （10）

                                                    （11）

由（3）、（9）、（10）、（11）各式得

。                                                         （12）

。                                                         （13）

对2球作同样的分析，沿垂直于轻杆方向球2与杆的相互作用力的大小与沿着轻杆方向球2与杆的相互作用力的大小分别为

，                                                         （14）

。                                                           （15）

由（12）、（14）式可知，杆与小球1、杆与小球2的最大静摩擦力相等，而（13）、（14）式表明小球1与杆的摩擦力大于小球2与杆的摩擦力，故在转动过程中，小球1与杆之间的摩擦力先达到最大静摩擦力，故小球1先滑动。设1球开始滑动时，细杆与水平线夹角为，则，

即，                                       （16）

由（16）式并代入数据得

。                                                                       （17）

当时，球1开始向外滑动。由于球1的初始位置紧靠轻杆末端，球1从开始滑动到脱离细杆的时间可忽略不计，因此球1脱离细杆与水平线夹角也为。

球1一旦脱离轻杆，因轻杆没有质量，球2与轻杆间的相互作用立即消失，此后球2只受重力作用而作斜舞女运动，注意到（2）、（3）、（7）各式，抛出时的初速度

。                                              （18）

初速度的方向与水平线的夹角

。                                                          （19）

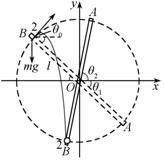
在球2作抛体运动的过程中，球与轻杆间虽无相互作用，但球仍套在杆上，轻杆将跟着球运动，但不会干扰小球的运动。当球离转轴的距离再次等于时，球2便脱离轻杆。建立如图所示的坐标系，根据斜抛运动规律可得任意时刻（取球2开始作抛体运动的时刻为计时起点）球2的位置坐标

，                                               （20）

，                                        （21）

球2脱离细杆时有

。                                                                      （22）

利用（17）、（18）、（19）各式得

，                                             （23）

从而解得

。                                                       （24）

此时

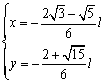。                                                      （25）

设球2脱离细杆时细杆与水平线夹角也为（如图），则

，                                               （26）

（或弧度）。            （27）

评分标准：（3）式2分，（7）式3分，（12）~（15）式各1分，（16）式2分，（17）式1分，（18）式2分，（19）式1分，（20）~（22）式各1分，（26）、（27）式各1分。