2020人教版(2019)高中物理专题练习137978
高中
整体难度：容易
2020-12-03
题号
一
二
三
四
五
评分
一、选择题 (共15题)
添加该题型下试题
1.
A、B两个质点，分别做匀速圆周运动，在相同的时间内它们通过的路程之比
，转过的角度之比
，则下列说法正确的是（ ）
A．它们的半径之比RA∶RB=2∶3 B．它们的半径之比RA∶RB=4∶9
C．它们的周期之比TA∶TB=2∶3 D．它们的周期之比TA∶TB=3∶2
难度：
知识点：圆周运动
使用次数：141
【答案】
C
【解析】
AB.A、B两质点分别做匀速圆周运动，在相同的时间内它们通过的路程之比，据
可得，它们的线速度之比：
vA∶vB=2∶3
A、B两质点转过的角度之比，据
可得，它们的角速度之比
据
，可得
则它们的轨道半径之比
选项AB错误；
CD.它们的角速度之比，根据
得：
选项C正确，D错误。
故选C。
2.
如图所示，一个小球绕圆心O做匀速圆周运动，已知圆周半径为R ， 该小球运动的线速度大小为v ， 则它运动的向心加速度大小为（ ）
A．v/R
B．νR
C．v2/R
D．νR2
难度：
知识点：向心加速度
使用次数：164
【答案】
C
【解析】
根据向心加速度的公式知，a=ω2r ．又v=ωr，故a=vω=v2/R，故C正确，ABD错误．故选C．
3.
如图所示为一皮带传动装置，右轮半径为r，a点在它的边缘上；左轮半径为2r，b点在它的边缘上．若在传动过程中皮带不打滑，则a点与b点的向心加速度大小之比（ ）
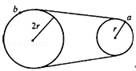
A．aa:ab=4:1 B．aa:ab=1:4
C．aa:ab=2:1 D．aa:ab=1:2
难度：
知识点：向心力
使用次数：178
【答案】
C
【解析】
试题分析：该图所示为皮带传送装置，所以A．b两点线速度相等
，由向心加速度
，可求出A．b两点向心加速度之比为2:1,C正确。
考点：皮带传动、向心加速度
4.
一质点以匀速率在水平面上做曲线运动，其轨迹如图所示
从图中可以看出，质点在a、b、c、d 四点处加速度最大的点是
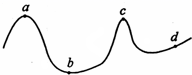
A．a B．b C．c D．d
难度：
知识点：向心加速度
使用次数：138
【答案】
C
【解析】
由图知c处曲率半径最小，质点的速率不变，由公式a=v2/r，知c点的加速度最大，故选C．
5.
A、B两艘快艇在湖面上做匀速圆周运动，在相同时间内，它们的路程之比为4:3，运动方向改变的角度之比为3:2，它们的向心加速度之比为（ ）
A．1:2 B．2:1 C．4:3 D．3:4
难度：
知识点：向心加速度
使用次数：161
【答案】
B
【详解】
根据题意可得它们的线速度：
它们的角速度之比为：
根据公式：
可得向心加速度之比为：
B正确。
故选B。
【点睛】
做此类题目的关键是对公式的灵活应用，匀速圆周运动这一块的公式比较多，所以一定要注意通过各个公式之间的联系来记忆。
本卷还有19题，登录并加入会员即可免费使用哦～
立即下载
全选试题
编辑试卷
收藏试卷
试题总数：
24
总体难度：
容易
难度统计
难度系数
数量
占比
容易
11
45.83%
基础
10
41.66%
偏难
1
4.16%
中等
2
8.33%
题型统计
大题类型
数量
占比
选择题
15
62.5%
填空题
5
20.83%
解答题
4
16.66%
知识点统计
知识点
数量
占比
圆周运动
12
50.0%
向心加速度
10
41.66%
向心力
1
4.16%
物理方法
1
4.16%
版权提示
该作品由: 用户小小分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益，请联系 可圈可点 ，我们核实后将及时进行处理。