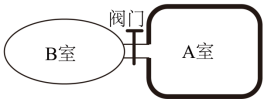
某些鱼类通过调节体内鱼鳔的体积实现浮沉。如图所示,鱼鳔结构可简化为通过阀门相连的 A 、 B 两个密闭气室, A 室壁厚、可认为体积恒定, B 室壁簿,体积可变;两室内气体视为理想气体,可通过阀门进行交换。质量为 M 的鱼静止在水面下 H 处。 B 室内气体体积为 V ,质量为 m ;设 B 室内气体压强与鱼体外压强相等、鱼体积的变化与 B 室气体体积的变化相等,鱼的质量不变,鱼鳔内气体温度不变。水的密度为 ρ ,重力加速度为 g 。大气压强为 p 0 ,求:
( 1 )鱼通过增加 B 室体积获得大小为 a 的加速度、需从 A 室充入 B 室的气体质量 D m ;
( 2 )鱼静止于水面下 H 1 处时, B 室内气体质量 m 1 。
答案
( 1 ) ;( 2 )
【详解】( 1 )由题知开始时鱼静止在 H 处,设此时鱼的体积为 ,有
且此时 B 室内气体体积为 V ,质量为 m ,则
鱼通过增加 B 室体积获得大小为 a 的加速度,则有
联立解得需从 A 室充入 B 室的气体质量
( 2 ) B 室内气体压强与鱼体外压强相等,则鱼静止在 H 处和水面下 H 1 处时, B 室内的压强分别为
,
由于鱼静止时,浮力等于重力,则鱼的体积不变,由于题可知,鱼体积的变化与 B 室气体体积的变化相等,则鱼在水下静止时, B 室内气体体积不变,由题知开始时鱼静止在 H 处时, B 室内气体体积为 V ,质量为 m ,由于鱼鳔内气体温度不变,若 ,则在 H 处时, B 室内气体需要增加,设吸入的气体体积为 Δ V ,根据玻意耳定律有
则此时 B 室内气体质量
若 ,则在 H 处时, B 室内气体需要减少,设释放的气体体积为 Δ V ,根据玻意耳定律有
则此时 B 室内气体质量



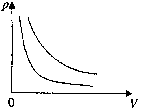
 图线为双曲线,同一气体的两条等温线比较,双曲线顶点离坐标原点远的温度高,即
图线为双曲线,同一气体的两条等温线比较,双曲线顶点离坐标原点远的温度高,即
 图线为过原点的直线,同一气体比较,斜率(
图线为过原点的直线,同一气体比较,斜率( 大的温度高,即
大的温度高,即 。
。
 ,求出每部分气体压强的变化量△p,并加以比较。
,求出每部分气体压强的变化量△p,并加以比较。