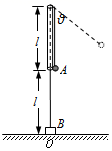
如图所示，长为3l的不可伸长的轻绳，穿过一长为l的竖直轻质细管，两端拴着质量分别为m、
m的小球A和小物块B，开始时B先放在细管正下方的水平地面上．手握细管轻轻摇动一段时间后，B对地面的压力恰好为零，A在水平面内做匀速圆周运动．已知重力加速度为g，不计一切阻力．
（1）求A做匀速圆周运动时绳与竖直方向夹角θ；
（2）求摇动细管过程中手所做的功；
（3）轻摇细管可使B在管口下的任意位置处于平衡，当B在某一位置平衡时，管内一触发装置使绳断开，求A做平抛运动的最大水平距离．
答案
（1）θ=45° ；（2）
；(3) 
。
【详解】
（1）B对地面刚好无压力，对B受力分析，得此时绳子的拉力为
对A受力分析，如图所示
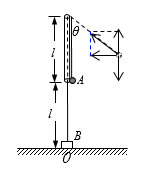
在竖直方向合力为零，故
解得
（2）对A球，根据牛顿第二定律有
解得
故摇动细管过程中手所做的功等于小球A增加的机械能，故有
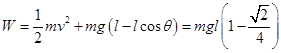
（3）设拉A的绳长为x（l≤x≤2l），根据牛顿第二定律有
解得
A球做平抛运动下落的时间为t，则有
解得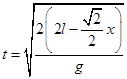
水平位移为
当
时，位移最大，为
