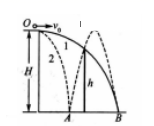
如图所示,从高H处的一点O先后平抛两个小球l和2.球1恰好直接掠过竖直挡板的顶端(未相碰)落到水平地面上的B点,球2则与地面处A点碰撞一次后,也恰好掠过竖直挡板落在B点.设球2与地面碰撞无机械能损失(类似遵循光的反射定律),则下列说法正确的是( )
A.球1平抛的初速度为球2的3倍
B.球1掠过挡板的时刻恰好是其做平抛运动从O到B的中间时刻
C.A点到挡板的距离是B点到挡板距离的 ![]()
D.竖直挡板的高度 ![]()
答案
ABD
【解析】
A项:球2运动轨迹可分为3段相同的平均轨迹,所以球2第一段一平抛的水平位移为![]() 是球1平抛轨迹水平位移
是球1平抛轨迹水平位移![]() 的三分之一,即
的三分之一,即![]() ,由于平抛高度h相同,由
,由于平抛高度h相同,由![]() 可知,时间相同,
可知,时间相同,![]() 可得两球水平初速度之比为3:1,故A正确;
可得两球水平初速度之比为3:1,故A正确;
B、C、D项:如图所示,设球1的初速度为v1,球2的初速度为v2,OA间的水平距离为d,由几何关系可知OB间的水平距离为3d,
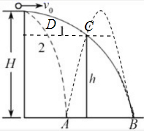
由分运动的等时性可知:球1从O点飞到挡板C点的时间与球2从O点飞到D点的时间相等;由对称性可知球2从O点飞到D点与由C飞到E的时间相等,OE两点间的水平距离为2d.球1从O点飞到C点与球2由C点飞到E点水平方向有:
![]()
解得:![]()
根据竖直方向的自由落体运动规律,连续相等时间内通过的位移之比为1:3,球1下落![]() 的时间刚好总时间的一半,故B正确,C错误,D正确.
的时间刚好总时间的一半,故B正确,C错误,D正确.
点晴:分析两小球的运动轨迹的特点,找出对称关系、几何关系以及等时关系式,列出式子是求解的关键.从以上的实例分析中我们看到,发现事物的对称性并利用运动的对称性去分析处理问题,可以大大地简化分析处理问题的过程,避开难点或冗长的数学推导,巧解问题.

 at2;
at2;

 =
= 。
。
 。
。 。
。
 。
。 及
及 得
得
 ,即A正确。由
,即A正确。由 得
得 ,则
,则 ,
, ,
, ,
,
 ,由此可知B正确。由
,由此可知B正确。由 得
得 ,即B点为AE段的时间中点,故
,即B点为AE段的时间中点,故 ,即C正确。对于匀变速直线运动,若时间相等,速度增量相等,故D错误,只有D符合题意。
,即C正确。对于匀变速直线运动,若时间相等,速度增量相等,故D错误,只有D符合题意。