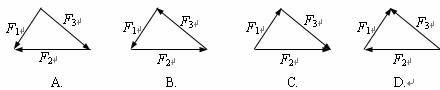
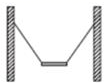
如图所示，用两根等长轻绳将木板悬挂在竖直木桩上等高的两点，制成一简易秋千．某次维修时将两轻绳各剪去一小段，但仍保持等长且悬挂点不变．用F1表示木板所受合力的大小，F2表示单根轻绳对木板拉力的大小，则维修后木板静止时（ ）
A．F1变大 B．F1变小 C．F2变大 D．F2变小
C
【解析】
试题分析：木板静止时，受重力和两个拉力而平衡，故三个力的合力为零，即：F1=0，不变；根据共点力平衡条件，有：2F2cosθ=mg，解得：F2=
，当细线变短时，细线与竖直方向的夹角θ增加，故cosθ减小，拉力F2变大．故选项A正确．
考点：力的动态平衡，合力的大小．
。 力的运算法则:
1．平行四边形定则
作用在同一点的两个互成角度的力的合力，不等于两分力的代数和，而是遵循平行四边形定则。如果以表示两个共点力F1和F2的线段为邻边作平行四边形，那么合力F的大小和方向就可以用这两个邻边之间的对角线表示，这叫做力的平行四边形定则，如图所示。 
2．三角形定则和多边形定则如图(a)所示，两力F1、F2合成为F的平行四边形定则，可演变为(b)图，我们将(b)图称为三角形定则合成图，即将两分力F1、F2首尾相接，则F就是由F，的尾端指向F2的首端的有向线段所表示的力。
如果是多个力合成，则由三角形定则合成推广可得到多边形定则，如图为三个力F1，F2、F3的合成图，F 为其合力。
登录并加入会员可无限制查看知识点解析
