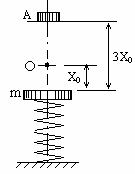
光滑水平轨道与半径为R的光滑半圆形轨道在B处连接，一质量为m2的小球静止在B处，而质量为m1的小球则以初速度v0向右运动，当地重力加速度为g，当m1与m2发生弹性碰撞后，m2将沿光滑圆形轨道上升，问：
（1）当m1与m2发生弹性碰撞后，m2的速度大小是多少？
（2）当m1与m2满足
，半圆的半径R取何值时，小球m2通过最高点C后，落地点距离B点最远．
答案
（1） 2m1v0/(m1+m2) （2） R=v02/2g(1+k)2
【解析】（1）以两球组成的系统为研究对象，
由动量守恒定律得：m1v0=m1v1+m2v2，
由机械能守恒定律得：
m1v02=m1v12+m2v22，
解得：
；
（2）小球m2从B点到达C点的过程中，
由动能定理可得：-m2g×2R=m2v2′2-m2v22，
解得：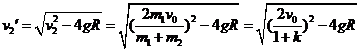
；
小球m2通过最高点C后，做平抛运动，
竖直方向：2R=gt2，
水平方向：s=v2′t，
解得：
，
由一元二次函数规律可知，当
时小m2落地点距B最远．
