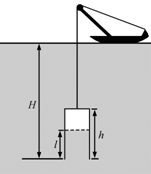
潜水钟是一种水下救生设备，它是一个底部开口、上部封闭的容器，外形与

当前位置：

学科首页

选修3 第二章气体、固体和液体

气体的等温变化

试题详情

难度：

使用次数：128

更新时间：2020-07-09

纠错

潜水钟是一种水下救生设备，它是一个底部开口、上部封闭的容器，外形与钟相似。潜水钟在水下时其内部上方空间里存有空气，以满足潜水员水下避险的需要。为计算方便，将潜水钟简化为截面积为S、高度为h、开口向下的圆筒；工作母船将潜水钟由水面上方开口向下吊放至深度为H的水下，如图所示。已知水的密度为ρ，重力加速度大小为g，大气压强为p₀，Hh，忽略温度的变化和水密度随深度的变化。

（1）求进入圆筒内水的高度l；

（2）保持H不变，压入空气使筒内水全部排出，求压入的空气在其压强为p₀时的体积。

查看答案

题型：计算题

知识点：气体的等温变化

下载试题

复制试题

【答案】

（1）；（2）

【详解】（1）设潜水钟在水面上方时和放入水下后筒内气体的体积分别为V₀和V₁，放入水下后筒内气体的压强为p₁，由玻意耳定律和题给条件有

p₁V₁= p₀V₀ ①

V₀=hS ②

V₁=（h–l）S ③

p₁= p₀+ ρg（H–l） ④

联立以上各式并考虑到Hh，h >l，解得

⑤

（2）设水全部排出后筒内气体的压强为p₂；此时筒内气体的体积为V₀，这些气体在其压强为p₀时的体积为V₃，由玻意耳定律有

p₂V₀= p₀V₃⑥

其中

p₂= p₀+ ρgH ⑦

设需压入筒内的气体体积为V，依题意

V = V₃–V₀⑧

联立②⑥⑦⑧式得

⑨

考点梳理:

根据可圈可点权威老师分析，试题“ ”主要考查你对玻意耳定律（等温定律）等考点的理解。关于这些考点的“资料梳理”如下：

◎ 玻意耳定律（等温定律）的定义

玻意耳定律:

1.概念:一定质量的某种气体，在温度不变的条件下其压强与体积变化时的关系，叫做气体的等温变化
2.规律:一定质量的气体，在温度不变的情况下，它的压强跟体积成反比—— 玻意耳定律3.公式:
4.图像:
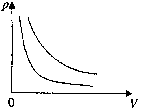
图线为双曲线，同一气体的两条等温线比较，双曲线顶点离坐标原点远的温度高，即图线为过原点的直线，同一气体比较，斜率(大的温度高，即。
5.条件：m一定，p不太大，T不太低
6.微观解释：一定质量的理想气体，分子的总数是一定的，在温度保持不变时，分子的平均动能保持不变，气体的体积减小到原来的几分之一，气体的密度就增大到原来的几倍，因此压强就增大到原来的几倍，反之亦然，所以气体的压强与体积成反比。

◎ 玻意耳定律（等温定律）的知识扩展

1、玻意耳定律描述了气体的等温变化规律，一定质量的某种气体，在温度不变的情况下，压强p与体积V成反比：pV=常量或p₁V₁=p₂V₂。
2、一定质量的某种气体，等温变化的p-V图象是双曲线，称为等温线。一定质量的气体，不同温度下的等温线不同。

◎ 玻意耳定律（等温定律）的知识点拨

液柱移动问题的求解方法：

液柱移动问题的分析方法
(1)假设推理法：根据题设条件，假设发生某种特殊的物理现象或物理过程，运用相应的物理规律及有关知识进行严谨的推理，得出正确的答案。巧用假设推理法可以化繁为简，化难为易，简捷解题。
(2)温度不变情况下的液柱移动问题的特点是：在保持温度不变的情况下改变其他题设条件，从而引起封闭气体液柱的移动，或液面的升降，或气体体积的增减。解决这类问题通常假设液柱不移动，或液面不升降，或气体体积不变，然后从假设出发，运用玻意耳定律等有关知识进行推论，求得正确答案。
(3)用液柱或活塞隔开两部分气体，当气体温度变化时，液柱或活塞是否移动?如何移动? 此类问题的特点是：气体的状态参量p、V、T都发生了变化，直接判断液柱或活塞的移动方向比较困难，通常先进行气体状态的假设，然后应用查理定律可以简单地求解：其一般思路为：
①先假设液柱或活塞不发生移动，两部分气体均做等容变化：
②对两部分气体分别应用查理定律的分比形式，求出每部分气体压强的变化量△p，并加以比较。
a．如果液柱两端的横截面积相等，且△p均大于零，意味着两部分气体的压强均增大，则液柱向△p值较小的一方移动；若△p均小于零，意味着两部分气体的压强均减小，则液柱向压强减小量较大的一方(即|△p|较大的一方)移动；若△p相等，则液柱不移动。
b．如果液柱两端的横截面积不相等，则应考虑液柱两端的受力变化(△pS)。，若△p均大于零，则液往向△pS较小的一方移动；若△p均小于零，则液桂向|△pS|值较大的一方移动；若△p等于零，则液柱不移动。

◎ 玻意耳定律（等温定律）的教学目标

1、知道什么是等温变化。
2、知道玻意耳定律是实验定律；掌握玻意耳定律的内容和公式；知道定律的适用条件。 3、理解气体等温变化的 p-V 图象的物理意义。
4、知道用分子动理论对玻意耳定律的定性解释。
5、会用玻意耳定律计算有关的问题。
6、通过对演示实验的研究，培养学生的观察、分析能力和从实验得出物理规律的能力。 7、渗透物理学研究方法的教育：当需要研究两个以上物理量间的关系时，先保持某个或某几个物理量不变，从最简单的情况开始研究，得出某些规律，然后再进一步研究所涉及的各个物理量间的关系。

◎ 玻意耳定律（等温定律）的考试要求

能力要求：应用
课时要求：60
考试频率：常考
分值比重：6

开通会员

登录并加入会员可无限制查看知识点解析

类题推荐：

气体的等温变化

难度：

使用次数：196

更新时间：2021-07-15

加入组卷

利用“验证玻意耳一马略特定律”的实验装置来验证查理定律．

（1）为了完成这个实验，除了图中给出的器材外，还需要气压计、托盘天平、热水、凉水和．
（2）必须进行的实验步骤有：

1．用托盘天平称出活塞和框架的质量M．用气压计读出实验室中的大气压强．按图安装器材，在框架两侧挂上钩码，使注射器的下半部分位于量杯之中．往量杯中加人适量的凉水，使注射器内的空气柱位于水面之下．过几分钟后，记下钩码的质量和活塞下表面的位置．同时．

2．在量杯中加些热水，过几分钟后在框架两侧加挂适当质量的钩码，使＿＿＿＿＿＿＿＿，记下钩码的质量．同时，．

3．把步骤2重复4次．

（3）可用作图法来验证查理定律是否成立，该图线的横坐标所代表的物理量及其单位是＿＿＿，纵坐标所代表的物理量及其单位是＿＿＿＿＿＿＿＿．

查看答案

题型：实验,探究题

知识点：气体的等温变化

复制

试题详情

纠错

难度：

使用次数：126

更新时间：2021-07-15

加入组卷

如图，一气缸竖直倒放，气缸内有一质量不可忽略的活塞，将一定量的理想气体封在气缸内，活塞与气缸壁元摩擦，气体处于平衡状态。现保持温度不变把气缸稍微倾斜一点，在达到平衡后，与原来相比，则

A．气体的压强变大

B．气体的压强变小

C．气体的体积变大

D．气体的体积变小

查看答案

题型：多项选择

知识点：气体的等温变化

复制

试题详情

纠错

难度：

使用次数：57

更新时间：2021-07-16

加入组卷

某同学用同一个注射器做了两次验证波意耳定律的实验，操作完全正确。根据实验数据却在P-V图上画出了两条不同双曲线。造成这种情况的可能原因是

A．两次实验中空气质量不同

B．两次实验中温度不同

C．两次实验中保持空气质量、温度相同，但所取的气体压的数据不同

D．两次实验中保持空气质量、温度相同，但所取的气体体的数据不同。

查看答案

题型：多项选择

知识点：气体的等温变化

复制

试题详情

纠错

难度：

使用次数：66

更新时间：2021-07-16

加入组卷

一个圆柱形的竖直的井里存有一定量的水，井的侧面和底部是密闭的，在井中固定地插着一根两端开口的薄壁圆管，管和井共轴，管下端未触及井底，在圆管内有一不漏气的活塞，它可沿圆管上下滑动，开始时，管内外水面相齐，且活塞恰好触及水面，如图所示，现用卷扬机通过绳子对活塞施加一个向上的力F，使活塞缓慢向上移动，已知管筒半径r=0.100m,井的半径R=2r，水的密度ρ=1.00×10³Kg/m³，大气压强为P₀=1.00×10³Pa，求活塞上升H=9.00m的过程中拉力F所做的功。（井和管在水面以上及水面以下的部分足够长，不计活塞质量，不计摩擦，重力加速度g=10m/s²）。