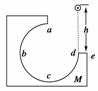
如图所示,M为固定在桌面上的异形木块,abcd为![]() 圆周的光滑轨道,a为轨道最高点,de面水平且与圆心等高.今将质量为m的小球在d点的正上方高为h处由静止释放,使其自由下落到d处后,又切入圆轨道运动,则下列说法正确的是( )
圆周的光滑轨道,a为轨道最高点,de面水平且与圆心等高.今将质量为m的小球在d点的正上方高为h处由静止释放,使其自由下落到d处后,又切入圆轨道运动,则下列说法正确的是( )
A.在h一定的条件下,释放后小球的运动情况与球的质量有关
B.只要改变h的大小,就能使小球在通过a点之后既可能落回轨道之内,又可能落到de面上
C.无论怎样改变h的大小,都不可能使小球在通过a点之后,又落回轨道之内
D.要使小球飞出de面之外(即落在e的右边)是可能的
答案
答案:CD
解析:只要小球能通过轨道的最高点a,即有va≥![]() ,小球能否落回轨道之内,取决于小球离开a点后做平抛运动的水平射程x,由平抛运动公式x=vat及R=
,小球能否落回轨道之内,取决于小球离开a点后做平抛运动的水平射程x,由平抛运动公式x=vat及R=![]() gt2得x≥
gt2得x≥![]() R,由此可知,小球通过a点之后,不可能落回轨道之内,但可能飞出de面之外.
R,由此可知,小球通过a点之后,不可能落回轨道之内,但可能飞出de面之外.