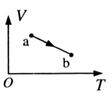
如图，一定量的理想气体从状态a沿直线变化到状态b，在此过程中，其压强
(A)逐渐增大 (B)逐渐减小
(C)始终不变 (D)先增大后减小
答案
A
如图，一定量的理想气体从状态a沿直线变化到状态b，在此过程中，其压强
(A)逐渐增大 (B)逐渐减小
(C)始终不变 (D)先增大后减小
A
玻意耳定律:
1.概念:一定质量的某种气体，在温度不变的条件下其压强与体积变化时的关系，叫做气体的等温变化
2.规律:一定质量的气体，在温度不变的情况下，它的压强跟体积成反比—— 玻意耳定律3.公式:
4.图像: 
图线为双曲线，同一气体的两条等温线比较，双曲线顶点离坐标原点远的温度高，即
图线为过原点的直线，同一气体比较，斜率(
大的温度高，即
。
5.条件：m一定，p不太大，T不太低
6.微观解释：一定质量的理想气体，分子的总数是一定的，在温度保持不变时，分子的平均动能保持不变，气体的体积减小到原来的几分之一，气体的密度就增大到原来的几倍，因此压强就增大到原来的几倍，反之亦然，所以气体的压强与体积成反比。
液柱移动问题的求解方法：
液柱移动问题的分析方法
(1)假设推理法：根据题设条件，假设发生某种特殊的物理现象或物理过程，运用相应的物理规律及有关知识进行严谨的推理，得出正确的答案。巧用假设推理法可以化繁为简，化难为易，简捷解题。
(2)温度不变情况下的液柱移动问题的特点是：在保持温度不变的情况下改变其他题设条件，从而引起封闭气体液柱的移动，或液面的升降，或气体体积的增减。解决这类问题通常假设液柱不移动，或液面不升降，或气体体积不变，然后从假设出发，运用玻意耳定律等有关知识进行推论，求得正确答案。
(3)用液柱或活塞隔开两部分气体，当气体温度变化时，液柱或活塞是否移动?如何移动? 此类问题的特点是：气体的状态参量p、V、T都发生了变化，直接判断液柱或活塞的移动方向比较困难，通常先进行气体状态的假设，然后应用查理定律可以简单地求解：其一般思路为：
①先假设液柱或活塞不发生移动，两部分气体均做等容变化：
②对两部分气体分别应用查理定律的分比形式
，求出每部分气体压强的变化量△p，并加以比较。
a．如果液柱两端的横截面积相等，且△p均大于零，意味着两部分气体的压强均增大，则液柱向△p值较小的一方移动；若△p均小于零，意味着两部分气体的压强均减小，则液柱向压强减小量较大的一方(即|△p|较大的一方)移动；若△p相等，则液柱不移动。
b．如果液柱两端的横截面积不相等，则应考虑液柱两端的受力变化(△pS)。，若△p均大于零，则液往向△pS较小的一方移动；若△p均小于零，则液桂向|△pS|值较大的一方移动；若△p等于零，则液柱不移动。
登录并加入会员可无限制查看知识点解析
