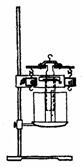
如图所示，竖直放置的气缸内盛有气体，上面被一活塞盖住，活塞通过劲度系数k＝600N/m的弹簧与气缸相连接，系统处于平衡状态，已知此时外界大气压强p0＝1.00×105N/m2，活塞到缸底的距离l＝0.500m，缸内横截面积S＝1.00×102m2，今在等温条件下将活塞缓慢上提到距缸底为2l处，此时提力为F＝500N，弹簧的原长l0应为多少？若提力为F＝700N，弹簧的原长l0又应为多少？
不计摩擦及活塞和弹簧的质量，并假定在整个过程中，气缸不漏气，弹簧都遵从胡克定律。
答案
解答一：
设弹簧的原长为
，气体原来压强为p，后来为p′，则由玻意耳定律可得
pl＝p′・2
①
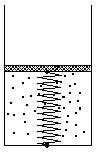
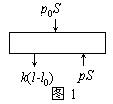
在原来状态下，活塞受力如图1所示，由力学平衡可得
pS＝p0S＋k(-) ②
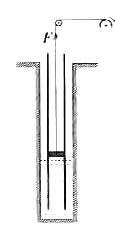
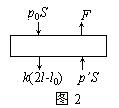
在后来状态下,活塞受力如图2所示,由力学平衡可得
p′S＋F＝p0S＋k(2－) ③
由①、②、③联立解得：
④
由式得： 
⑤
当F＝500N时，由④式得p＝0.4p0 再代入⑤式得＝1.50m，可见在整个过程中弹簧始终处于压缩状态。
当F＝700N时，由④式得p＝0.8p0 再代入⑤式得＝0.833m，可见在过程开始时弹簧处于压缩状态，当活塞提高到距缸底距离超过＝0.833m后，弹簧被拉伸。
解答二：
设开始时弹簧的压缩量为
(当得出为负值．则表示开始时弹簧被拉长)，原长为。依题意得方程：
p0S＝pS＋kx ①
p0S＝p′S－k(－2x)＋F ②
p′S・2(l0－x) ＝pS(－x) ③
＝l＋x ④
由①、②、③、④式联立，解得：
⑤
当F＝500 N时，代入⑤式，得x＝1.00 m，＝1.50 m。
当F＝700 N时，代入⑤式，得x＝0.333 m，＝0.833 m。
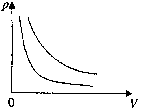
图线为双曲线，同一气体的两条等温线比较，双曲线顶点离坐标原点远的温度高，即
图线为过原点的直线，同一气体比较，斜率(
大的温度高，即
。
，求出每部分气体压强的变化量△p，并加以比较。
