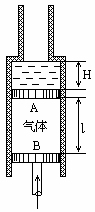
如图所示,有一个直立的气缸,气缸底到气缸口的距离为L0厘米,用一厚度和质平衡时活塞上表面与气缸口的距离很小(计算时可忽略不计),周围大气的压强为H0厘米水银柱.现把盛有水银的一个瓶子放在活塞上(瓶子的质量可忽略),平衡时活塞到气缸底的距离为L厘米.若不是把这瓶水银放在活塞上,而是把瓶内水银缓缓不断地倒在活塞上方,这时活塞向下移,压缩气体,直到活塞不再下移.
求此时活塞在气缸内可能的位置以及与之相对应的条件(即题中给出量之间应满足的关系).设气体的温度不变. 
答案
解:设整瓶水银放在活塞上后,使气缸内气体增加的压强为h厘米水银柱,由玻意耳-马略特定律H0L0=(H0+h)L, (1)
得![]() (2)
(2)
h的大小反映了水银质量的大小.
当水银注入后,活塞不再下移时,设活塞上水银的深度为△H厘米,活塞下移的距离为△x厘米,则由玻意耳-马略特定律
H0L0=(H0+△H)(L0-△x), (3)
解得![]() (4)
(4)
可能发生两种情况:
(1).水银比较少,瓶内水银全部注入后,尚未灌满或刚好灌满活塞上方的气缸,这时 △H=h, (5) △H≤△x, (6)
由(2)、(4)、(5)三式,得 △x=L0-L, (7)
活塞到气缸底的距离 L′=L0-△x=L, (8)
由(4)、(6)、(7)三式,得 L≥H0, (9)
即若L≥H0,则L′=L.
(2).瓶内水银比较多,当活塞上方的气缸灌满水银时,瓶内还剩有一定量的水银,这时 △H=△x, (10) △H<h, (11)
由(4)、(10)两式,得△x=L0-H0, (12)
活塞到气缸底的距离 L′=L0-△x=H0, (13)
由(2)、(10)、(11)三式,得L<H0. (14)
即若L<H0,则L′=H0.