2020天津人教版(2019)高中物理高考模拟138344
高中
整体难度：中等
2021-01-12
题号
一
二
三
四
五
评分
一、选择题 (共16题)
添加该题型下试题
1.
下列说法正确的是（ ）
A．同种元素的固体，可能由于原子（或分子）的排列方式不同而成为不同的晶体
B．悬浮微粒越大，在某一瞬间撞击它的液体分子数越多，布朗运动越明显
C．系统不可能从单一热源吸热全部用于做功
D．布料做成的雨伞，纤维间虽然有缝隙，但是不漏雨，原因是雨水和布料浸润
难度：
知识点：热力学第二定律
使用次数：114
【答案】
A
【详解】
A．同种元素的固体，可能由于原子（或分子）的排列方式不同而成为不同的晶体，如石墨和金刚石，A正确；
B．悬浮微粒越小，液体分子对微粒撞击造成的不平衡性越大，布朗运动越明显，B错误；
C．在引起外界变化的情况下，系统可以从单一热源吸热全部用于做功，C错误；
D．布料（与雨水不浸润）做成的雨伞，纤维间虽然有缝隙，但是不漏雨，原因是液体的表面张力使得雨滴表面收缩，不易穿过雨伞的缝隙，D错误。
故选A。
2.
某实验小组用同一光电管完成了光电效应实验，得到了光电流与对应电压之间的关系图像甲、乙、丙，如图所示。则下列说法正确的是（ ）
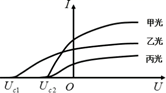
A．甲光的频率大于乙光的频率
B．乙光的波长大于丙光的波长
C．甲光的光强大于丙光的光强
D．甲光和丙光产生的光电子的最大初动能不相等
难度：
知识点：光电效应
使用次数：122
【答案】
C
【详解】
A．根据eUc=Ek=hv-W0，入射光的频率越高，对应的遏止电压Uc越大。甲光的遏止电压小于乙光，所以甲光频率小于乙光的频率，故A错误；
B．丙光的遏止电压小于乙光的遏止电压，所以丙光的频率小于乙光的频率，则乙光的波长小于丙光的波长，故B错误；
C．由于甲光的饱和光电流大于丙光饱和光电流，两光频率相等，所以甲光的强度高于丙光的强度，故C正确；
D．甲光的遏止电压等于丙光的遏止电压，由Ekm=e•U遏可知，甲光对应的光电子最大初动能等于丙光的光电子最大初动能。故D错误；
故选C。
3.
理想变压器原线圈两端输入的交变电流电压如图所示，变压器原、副线圈的匝数比为5 ： 1，如图乙所示，定值电阻R0 = 10 Ω，R为滑动变阻器，则下列说法正确的是（ ）
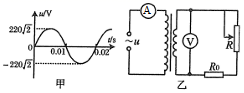
A．电压表的示数为
B．变压器输出电压频率为10 Hz
C．当滑动变阻器滑片向下移动时，变压器的输入功率增大
D．当滑动变阻器滑片向下移动时，电流表的示数减小
难度：
知识点：变压器
使用次数：242
【答案】
C
【详解】
A． 原线圈电压有效值为220V，根据电压与匝数成正比知电压表示数为44V，故A错误；
B． 由甲图知周期0.02s，则
变压器不改变交变电流的频率，故B错误；
CD． 滑动触头P向下移动，电阻变小，输入电压和匝数不变，则副线圈电压不变，电流增加，输出功率增大，故输入功率等于输出功率增加，输入电压不变，则原线圈电流增大，故电流表示数变大，故C正确D错误。
故选：C。
4.
在人类太空征服史中，让人类遗憾的是“太空加油站”的缺乏。当通信卫星轨道校正能源耗尽的时候，它的生命就走到了尽头，有很多成了太空垃圾。如今“轨道康复者”是救助此类卫星的新型太空航天器，图甲是“轨道康复者”航天器在给太空中“垃圾”卫星补充能源，可简化为图乙所示的模型，让“轨道康复者”N对已偏离原来正常工作轨道的卫星M进行校正，则（ ）
A．“轨道康复者”N从图乙所示轨道上加速，与卫星M对接补充能源后开动M上的小发动机向前喷气，能校正卫星M到较低的轨道运行
B．让M降低到N所在轨道上，补充能源后再开启卫星M上的小发动机校正
C．在图乙中M的动能一定小于N的动能
D．在图乙中，M、N和地球球心三者不可能处在同一直线上
难度：
知识点：宇宙航行
使用次数：157
【答案】
A
【详解】
A．开动M上的小发动机向前喷气，可使卫星M减速，速度减小，所需的向心力减小，卫星M做向心运动，则能校正卫星M到较低的轨道运行，故A正确；
B．让M降低到N所在轨道上，补充能源后再开启卫星M上的小发动机，可使卫星M减速，速度减小，所需的向心力减小，卫星M做向心力运动，则卫星M会在更低的轨道运动，故B错误；
C．由于不知道M、N的质量，所以无法比较两者的动能，故C错误；
D．由
可得
可知
N的角速度比M的大，所以M、N和地球球心三者可能处在同一直线上，故D错误。
故选A。
5.
如图所示，两个可视为质点的小球A、B通过固定在O点的光滑滑轮用轻绳相连，小球A置于光滑半圆柱上，小球B用水平轻绳拉着，水平轻绳另一端系于竖直板上，两球均处于静止状态。已知O点在半圆柱横截面圆心O1的正上方，OA与竖直方向成30°角、其长度与半圆柱横截面的半径相等，OB与竖直方向成60°角，则（ ）
A．轻绳对球A的拉力与球A所受弹力的合力大小相等
B．轻绳对球A的拉力与半网柱对球A的弹力大小不相等
C．轻绳AOB对球A的拉力与对球B的拉力大小之比为
：
D．球A与球B的质量之比为2：1
难度：
知识点：力的合成和分解
使用次数：262
【答案】
D
【详解】
设轻绳中拉力为T，球A受力如图
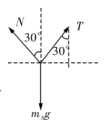
A．所受弹力为绳对A的拉力和半圆对球A的弹力的合力，与重力等大反向，大于T，故A错误；
B．受力分析可得
解得
故B错误；
C．细线对A的拉力与对球B的拉力都等于T，故C错误；
D．对球B
解得
故D正确。
故选D。
本卷还有20题，登录并加入会员即可免费使用哦～
立即下载
全选试题
编辑试卷
收藏试卷
试题总数：
25
总体难度：
中等
难度统计
难度系数
数量
占比
容易
10
40.0%
中等
13
52.0%
偏难
2
8.0%
题型统计
大题类型
数量
占比
选择题
16
64.0%
实验,探究题
3
12.0%
解答题
6
24.0%
知识点统计
知识点
数量
占比
热力学第二定律
1
4.0%
光电效应
2
8.0%
变压器
1
4.0%
宇宙航行
1
4.0%
力的合成和分解
1
4.0%
温度和温标
1
4.0%
交变电流的描述
1
4.0%
共点力的平衡
1
4.0%
电势能和电势
1
4.0%
氢原子光谱和玻尔的原子模型
1
4.0%
波的描述
1
4.0%
电场 电场强度
1
4.0%
原子的核实结构模型
1
4.0%
波的形成
1
4.0%
牛顿第二定律
1
4.0%
牛顿运动定律的应用
2
8.0%
重力与弹力
1
4.0%
实验：电池电动势和内阻的测量
1
4.0%
能量守恒定律
1
4.0%
带电粒子在匀强磁场中的运动
2
8.0%
专题八 电磁感应
1
4.0%
电磁感应现象与应用
1
4.0%
版权提示
该作品由: 用户828305分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益，请联系 可圈可点 ，我们核实后将及时进行处理。