2019高一上学期人教版(2019)高中物理单元测试138040
高中
整体难度：中等
2020-12-22
题号
一
二
三
四
五
评分
一、选择题 (共70题)
添加该题型下试题
1.
弹簧振子做简谐运动，其振动图象如图所示，则：
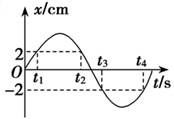
A．t1、t2时刻振子的速度大小相等，方向相反
B．t1、t2时刻振子加速度大小相等，方向相反
C．t2、t3时刻振子的速度大小相等，方向相反
D．t2、t3时刻振子的加速度大小相等，方向相同
难度：
知识点：简谐运动
使用次数：100
【答案】
A
【详解】
A由图线可知，t1、t2时刻振子的速度大小相等，方向相反，选项A正确；
B．t1、t2时刻振子位移相同，故恢复力相同，加速度大小相等，方向相同，选项B错误；
C．t2、t3时刻振子的速度大小相等，方向相同，均向下，选项C错误；
D．t2、t3时刻振子的加速度大小相等，方向相反，选项D错误；
故选A.
2.
如图所示，用高压水枪喷出的强力水柱冲击煤层，设水柱直径为D，水流速度大小为
，方向水平向右．水柱垂直煤层表面，水柱冲击煤层后水的速度变为零，水的密度为
，高压水枪的重力不可忽略，手持高压水枪操作，下列说法正确的是
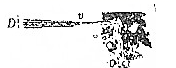
A．水枪单位时间内喷出水的质量为
B．高压水枪的喷水功率为
C．水柱对煤层的平均冲击力大小为
D．手对高压水枪的作用力水平向右
难度：
知识点：动量定理
使用次数：169
【答案】
BD
【详解】
A、t时间内喷水质量为：
水枪单位时间内喷出水的质量为
故选项A错误；
B、水枪在时间1s内做功转化为水柱的动能即为高压水枪的喷水功率，则：
故选项B正确；
C、t时间内喷出的水在t内速度减小为0，则由动量定理得：
联立得：
，
故选项C错误；
D、水对高压水枪的作用力向左，则手对高压水枪的作用力水平向右，故选项D正确．
3.
一物体放在水平地面上，如图1所示，已知物体所受水平拉力F随时间t的变化情况如图2所示，物体相应的速度v随时间t的变化关系如图3所示，则（ ）
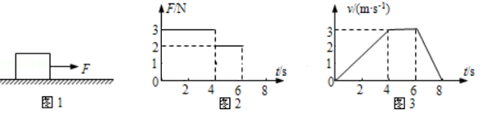
A．0~8s时间内水平拉力的冲量大小为零
B．0~6s时间内合外力的冲量大小为 4N·s
C．t=4s时物体的动量大小为4kg·m/s
D．0~8s时间内物体克服摩擦力所做的功30J
难度：
知识点：动能和动能定律
使用次数：110
【答案】
BCD
【详解】
A、由图象知，力F的方向恒定，故力F在0～8s内的冲量I=F1t1+F2t2+F3t3=3×4+2×2+0×2N•s=16N•s；方向向右，故A错误．B、由4~6s物体匀速直线运动可知
，则0~6s的
，故B正确．C、因0~4s的
，根据动量定理可知动量变化为4N·s，而初动量为零，则4s末的动量为4kg.m/s，故C正确．D、由
图象的面积代表位移，可求得0~8s的位移为
，根据功的定义式可得
，故D正确．故选BCD．
【点睛】
此题考查了学生对图象问题的分析能力，能从图象中得出相关的信息，然后结合动能定理和动量定理的计算公式进行计算求解，是高考的热点考题．
4.
如图所示，质量为m的小球从距离地面高度为H的A点由静止释放，落到地面上后又陷入泥潭中，由于受到阻力作用，到达距地面深度为h的B点时速度减为零不计空气阻力，重力加速度为g。则关于小球下落过程中，说法正确的是
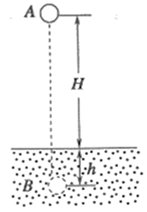
A．整个下落过程中，小球的机械能减少了mgH
B．整个下落过程中，小球克服阻力做的功为mg(H+h)
C．在陷入泥潭过程中，小球所受阻力的冲量大于m
D．在陷入泥潭过程中，小球动量的改变量的大小等于m
难度：
知识点：能量守恒定律
使用次数：176
【答案】
BCD
【解析】
A.小球在整个过程中，动能变化量为零，重力势能减小mg(H+h），则小球的机械能减小了mg(H+h);故A错误.
B.对全过程运用动能定理得，mg(H+h)-Wf=0，则小球克服阻力做功Wf=mg(H+h);故B正确.
C.落到地面的速度
，对进入泥潭的过程取向下为正方向，运用动量定理得，IG-If=0-mv，知阻力的冲量大小
，则小球所受阻力的冲量大于m
;故C正确.
D.落到地面的速度，对进入泥潭后的速度为0，所以小球动量的改变量大小等于m;故D正确.
5.
如图甲,质量M=0.8 kg 的足够长的木板静止在光滑的水平面上,质量m=0.2 kg的滑块静止在木板的左端,在滑块上施加一水平向右、大小按图乙所示随时间变化的拉力F,4 s后撤去力F。若滑块与木板间的动摩擦因数μ=0.2,最大静摩擦力等于滑动摩擦力,重力加速度g=10 m/s2,则下列说法正确的是
A．0~4s时间内拉力的冲量为3.2 N·s B．t= 4s时滑块的速度大小为9.5 m/s
C．木板受到滑动摩擦力的冲量为2.8 N·s D．2~4s内因摩擦产生的热量为4J
难度：
知识点：牛顿运动定律的应用
使用次数：191
【答案】
BCD
【详解】
A.冲量的定义式：
，所以F-t图像面积代表冲量，所以0-4 s时间内拉力的冲量为
故A错误；
B.木块相对木板滑动时：对木板：
对木块：
联立解得：
，
所以0时刻，即相对滑动，对滑块：
解得4s时滑块速度大小：
故B正确；
C.4s时，木板的速度
撤去外力后，木板加速，滑块减速，直到共速，根据动量守恒：
解得：
，
对木板根据动量定理可得：
故C正确；
D.0-2s内，对m：
解得：
对M
解得v2=1m/s
2-4s内：对m
；
对M
所以
故D正确。
本卷还有95题，登录并加入会员即可免费使用哦～
立即下载
全选试题
编辑试卷
收藏试卷
试题总数：
100
总体难度：
中等
难度统计
难度系数
数量
占比
容易
24
24.0%
中等
47
47.0%
偏难
20
20.0%
基础
9
9.0%
题型统计
大题类型
数量
占比
选择题
70
70.0%
解答题
5
5.0%
实验,探究题
20
20.0%
填空题
5
5.0%
知识点统计
知识点
数量
占比
简谐运动
17
17.0%
牛顿第二定律
1
1.0%
实验：用单摆测量重力加速度
20
20.0%
单摆
5
5.0%
动量定理
10
10.0%
动能和动能定律
5
5.0%
能量守恒定律
1
1.0%
牛顿运动定律的应用
4
4.0%
受破振动 共振
15
15.0%
波的描述
1
1.0%
动量
9
9.0%
机械能守恒定律
2
2.0%
行星的运动
1
1.0%
重力势能
1
1.0%
功与功率
4
4.0%
自由落体运动
1
1.0%
圆周运动
1
1.0%
波的形成
1
1.0%
弹性碰撞和非弹性碰撞
1
1.0%
版权提示
该作品由: 用户潘诚分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益，请联系 可圈可点 ，我们核实后将及时进行处理。