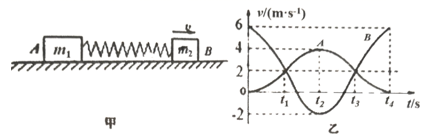
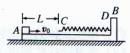
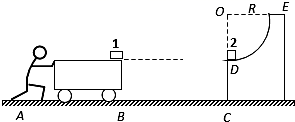
如图所示, “L” 型平板 B 静置在地面上,小物块 A 处于平板 B 上的 点,
点左侧粗糙,右侧光滑。用不可伸长的轻绳将质量为 M 的小球悬挂在
点正上方的 O 点,轻绳处于水平拉直状态。将小球由静止释放,下摆至最低点与小物块 A 发生碰撞,碰后小球速度方向与碰前方向相同,开始做简谐运动(要求摆角小于
), A 以速度
沿平板滑动直至与 B 右侧挡板发生弹性碰撞。一段时间后, A 返回到 O 点的正下方时,相对于地面的速度减为零,此时小球恰好第一次上升到最高点。已知 A 的质量
, B 的质量
, A 与 B 的动摩擦因数
, B 与地面间的动摩擦因数
,取重力加速度
。整个过程中 A 始终在 B 上,所有碰撞时间忽略不计,不计空气阻力,求:
( 1 ) A 与 B 的挡板碰撞后,二者的速度大小 与
;
( 2 ) B 光滑部分的长度 d ;
( 3 )运动过程中 A 对 B 的摩擦力所做的功 ;
( 4 )实现上述运动过程, 的取值范围(结果用
表示)。
答案
( 1 ) ,
;( 2 )
;( 3 )
;( 4 )
【详解】( 1 )设水平向右为正方向,因为 点右侧光滑,由题意可知 A 与 B 发生弹性碰撞,故碰撞过程根据动量守恒和能量守恒有
代入数据联立解得
,(方向水平向左)
,(方向水平向右)
即 A 和 B 速度的大小分别为 ,
。
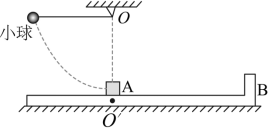
( 2 )如图所示为 A 与 B 挡板碰撞后到运动至 O 点正下方的运动示意图
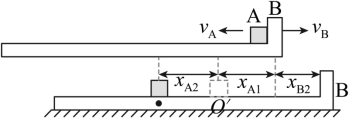
A 回到 前, A 在 B 上匀速直线运动的时间设为
。 A 的位移大小
对平板 B ,由牛顿第二定律得
对平板 B ,由运动学公式有
由几何关系
①
A 从 回到 O 点正下方设时间为
, A 在 B 上做匀减速直线运动,设 A 的加速度大小为
,由牛顿第二定律得
解得
A 返回到 O 点的正下方时,相对于地面的速度减为零,则
时间内 A 相对于地面的位移大小
由几何关系
②
联立解得
或
,
由 ①② 可得
与
等大
分析可知, A 回到 O 点正下方时 B 未减速为 0 ,故
舍去。综上解得
( 3 )在 A 刚开始减速时, B 物体的速度为
在 A 减速过程中,对 B 分析根据牛顿运动定律可知
解得
B 物体停下来的时间为 t 3 ,则有
解得
可知在 A 减速过程中 B 先停下来了,此过程中 B 的位移为
所以 A 对 B 的摩擦力所做的功为
( 4 )小球和 A 碰撞后 A 做匀速直线运动再和 B 相碰,此过程有
由题意可知 A 返回到 O 点的正下方时,小球恰好第一次上升到最高点,设小球做简谐振动的周期为 T ,摆长为 L ,则有
由单摆周期公式 解得,小球到悬挂点 O 点的距离
小球下滑过程根据动能定理有
当碰后小球摆角恰为 5° 时,有
解得
,
小球与 A 碰撞过程根据动量守恒定律有
小球与 A 碰后小球速度方向与碰前方向相同,开始做简谐运动(要求摆角小于 ),则要求
故要实现这个过程的范围为