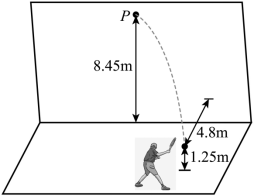
如图所示，某同学将离地的网球以

当前位置：

学科首页

必修2 第五章抛体运动

抛体运动的规律

试题详情

难度：

使用次数：101

更新时间：2023-07-05

纠错

如图所示，某同学将离地的网球以的速度斜向上击出，击球点到竖直墙壁的距离。当网球竖直分速度为零时，击中墙壁上离地高度为的 P 点。网球与墙壁碰撞后，垂直墙面速度分量大小变为碰前的 0.75 倍。平行墙面的速度分量不变。重力加速度 g 取，网球碰墙后的速度大小 v 和着地点到墙壁的距离 d 分别为（　　）

A ． B ． C ． D ．

查看答案

题型：选择题

知识点：抛体运动的规律

下载试题

复制试题

【答案】

【详解】设网球飞出时的速度为，竖直方向

代入数据得

则

排球水平方向到点的距离

根据几何关系可得打在墙面上时，垂直墙面的速度分量

平行墙面的速度分量

反弹后，垂直墙面的速度分量

则反弹后的网球速度大小为

网球落到地面的时间

着地点到墙壁的距离

故 BD 正确， AC 错误。

故选 BD 。

考点梳理:

根据可圈可点权威老师分析，试题“ ”主要考查你对匀变速直线运动规律的应用等考点的理解。关于这些考点的“资料梳理”如下：

◎ 匀变速直线运动规律的应用的定义

基本公式：

①速度公式：v_t=v₀+at；
②位移公式：s=v₀t+at²；
③速度位移公式：v_t²-v₀²=2as。

推导公式：
①平均速度公式：V=。
②某段时间的中间时刻的瞬时速度等于该段时间内的平均速度：。
③某段位移的中间位置的瞬时速度公式：。无论匀加速还是匀减速，都有。
④匀变速直线运动中，在任意两个连续相等的时间T内的位移差值是恒量，即ΔS=S_n+l–S_n=aT²=恒量。
⑤初速为零的匀变速直线运动中的比例关系（设T为相等的时间间隔，s为相等的位移间隔）：
Ⅰ、T末、2T末、3T末……的瞬时速度之比为：v₁：v₂：v₃：……：v_n=1：2：3：……：n；
Ⅱ、T内、2T内、3T内……的位移之比为：s₁：s₂：s₃：……：s_n=1：4：9：……：n²；
Ⅲ、第一个T内、第二个T内、第三个T内……的位移之比为：s_Ⅰ：s_Ⅱ：s_Ⅲ：……：s_N=1：3：5：……：(2N-1)；
Ⅳ、前一个s、前两个s、前三个s……所用的时间之比为：t₁：t₂：t₃：……：t_n=1：……：；
Ⅴ、第一个s、第二个s、第三个s……所用的时间之比为t_Ⅰ、t_Ⅱ、t_Ⅲ：……：t_N=1：……：。

◎ 匀变速直线运动规律的应用的知识扩展

1、基本公式：
①速度公式：v_t=v₀+at；
②位移公式：s=v₀t+

at²；
③速度位移公式：v_t²-v₀²=2as。
2、推导公式：
①平均速度公式：V=

。
②某段时间的中间时刻的瞬时速度等于该段时间内的平均速度：

。
③某段位移的中间位置的瞬时速度公式：

。无论匀加速还是匀减速，都有

。
④匀变速直线运动中，在任意两个连续相等的时间T内的位移差值是恒量，即ΔS=S_n+l–S_n=aT²=恒量。
⑤初速为零的匀变速直线运动中的比例关系（设T为相等的时间间隔，s为相等的位移间隔）：
Ⅰ、T末、2T末、3T末……的瞬时速度之比为：v₁：v₂：v₃：……：v_n=1：2：3：……：n；
Ⅱ、T内、2T内、3T内……的位移之比为：s₁：s₂：s₃：……：s_n=1：4：9：……：n²；
Ⅲ、第一个T内、第二个T内、第三个T内……的位移之比为：s_Ⅰ：s_Ⅱ：s_Ⅲ：……：s_N=1：3：5：……：(2N-1)；
Ⅳ、前一个s、前两个s、前三个s……所用的时间之比为：t₁：t₂：t₃：……：t_n=1：

……：

；
Ⅴ、第一个s、第二个s、第三个s……所用的时间之比为t_Ⅰ、t_Ⅱ、t_Ⅲ：……：t_N=1：

……：

。
3、追及相遇问题
①当两个物体在同一直线上运动时，由于两物体的运动情况不同，所以两物体之间的距离会不断发生变化，两物体间距会越来越大或越来越小，这时就会涉及追及、相遇或避免碰撞等问题。
②追及问题的两类情况：
Ⅰ、速度大者减速（如匀减速直线运动）追速度小者（如匀速运动）：

Ⅱ、速度小者加速（如初速度为零的匀加速直线运动）追速度大者（如匀速运动）：

③相遇问题的常见情况：
Ⅰ、同向运动的两物体追及即相遇；
Ⅱ、相向运动的物体，当各自发生的位移大小和等于开始时两物体的距离时即相遇。

◎ 匀变速直线运动规律的应用的特性

追及相遇问题：

①当两个物体在同一直线上运动时，由于两物体的运动情况不同，所以两物体之间的距离会不断发生变化，两物体间距会越来越大或越来越小，这时就会涉及追及、相遇或避免碰撞等问题。
②追及问题的两类情况：
Ⅰ、速度大者减速（如匀减速直线运动）追速度小者（如匀速运动）：

Ⅱ、速度小者加速（如初速度为零的匀加速直线运动）追速度大者（如匀速运动）：

③相遇问题的常见情况：
Ⅰ、同向运动的两物体追及即相遇；
Ⅱ、相向运动的物体，当各自发生的位移大小和等于开始时两物体的距离时即相遇。

◎ 匀变速直线运动规律的应用的知识点拨

知识点拨：

例：如图所示，光滑斜面AE被分为四个长度相等的部分，即AB=BC=CD=DE，一物体由A点静止释放，下列结论不正确的是（）

A. 物体到达各点的速率之比=。

B. 物体到达各点所经历的时间。

C. 物体从A运动到E的全过程的平均速度。

D. 物体通过每一部分时，其速度增量。

解析：由及得，即A正确。由得，则，，，，由此可知B正确。由得，即B点为AE段的时间中点，故，即C正确。对于匀变速直线运动，若时间相等，速度增量相等，故D错误，只有D符合题意。

答案：Ｄ

◎ 匀变速直线运动规律的应用的教学目标

1．知识与能力
（1）掌握匀变速直线运动的基本公式，并能恰当选择这些公式解决物理问题．
（2）能够熟练应用匀变速直线运动的重要推论解决物理问题。
（3）培养学生运用方程组、图像等数学工具解决物理问题的能力。
（4）通过一题多解培养学生发散思维。
2．过程和方法
（1）通过例题的分析，使学生形成解题思路，体会特殊解题技巧，即获得解决物理问题的认知策略。
（2）渗透物理思想方法的教育，如模型方法、等效方法等。
3．情感态度与价值观
通过对实际生活中直线运动的研究，保持对运动世界的好奇心和探究欲。

◎ 匀变速直线运动规律的应用的考试要求

能力要求：应用
课时要求：120
考试频率：必考
分值比重：5

开通会员

登录并加入会员可无限制查看知识点解析

类题推荐：

抛体运动的规律

难度：

使用次数：87

更新时间：2021-07-13

加入组卷

如图所示，在“研究平抛物体运动”的实验中，用一张印有小方格的纸记录轨迹，小方格的边长L=1.25cm。若小球在平抛运动途中的几个位置如图中的a、b、c、d所示，则小球平抛的初速度的计算式为v_o=　　　　　　（用L、g表示），其值是　　　　　（取g=9.8m/s²），小球在b点的速率是　　　　　　。

查看答案

题型：填空题

知识点：抛体运动的规律

复制

试题详情

纠错

难度：

使用次数：143

更新时间：2021-07-13

加入组卷

如图6所示，MN为竖直屏幕，从O点一小球以某一速度水平抛出打在A点正下方B点，A点与O点在同一水平高度，在小球抛出后的运动过程中，若加竖直向下的平行光，则小球的影子在水平地面上的运动是运动；若加水平向左方向的平行光，则小球的影子在MN上的运动是运动；若在小球抛出的同时，在O点有一点光源，则小球的影子在AB之间的运动是运动。