半径为 R 的绝缘细圆环固定在图示位置，圆心位于 O 点，环上均匀分布着电量为 Q 的正电荷。点 A 、 B 、 C 将圆环三等分，取走 A 、 B 处两段弧长均为 的小圆弧上的电荷。将一点电荷 q 置于 延长线上距 O 点为 的 D 点， O 点的电场强度刚好为零。圆环上剩余电荷分布不变， q 为（　　）

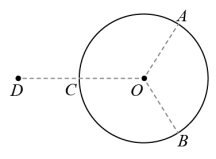
A ．正电荷， B ．正电荷，

C ．负电荷， D ．负电荷，

答案

C

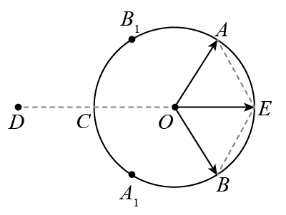
【详解】取走 A 、 B 处两段弧长均为 的小圆弧上的电荷，根据对称性可知，圆环在 O 点产生的电场强度为与 A 在同一直径上的 A ₁ 和与 B 在同一直径上的 B ₁ 产生的电场强度的矢量和，如图所示，因为两段弧长非常小，故可看成点电荷，则有

由图可知，两场强的夹角为 ，则两者的合场强为

根据 O 点的合场强为 0 ，则放在 D 点的点电荷带负电，大小为

根据

联立解得

故选 C 。