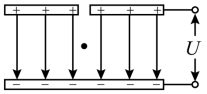
密立根油滴实验装置如图所示，两块水平放置的金属板分别与电源

当前位置：

学科首页

必修3 第十章静电场中的能量

带电粒子在电场中的运动

试题详情

难度：

使用次数：169

更新时间：2023-06-29

纠错

密立根油滴实验装置如图所示，两块水平放置的金属板分别与电源的正负极相接，板间产生匀强电场。用一个喷雾器把密度相同的许多油滴从上板中间的小孔喷入电场，油滴从喷口喷出时由于摩擦而带电。金属板间电势差为 U 时，电荷量为 q 、半径为 r 的球状油滴在板间保持静止。若仅将金属板间电势差调整为 2 U ，则在板间能保持静止的球状油滴所带电荷量和半径可以为（　　）

A ． q ， r B ． 2 q ， r C ． 2 q ， 2 r D ． 4 q ， 2 r

查看答案

题型：选择题

知识点：带电粒子在电场中的运动

下载试题

复制试题

【答案】

【详解】初始状态下，液滴处于静止状态时，满足

即

AB ．当电势差调整为 2 U 时，若液滴的半径不变，则满足

可得

AB 错误；

CD ．当电势差调整为 2 U 时，若液滴的半径变为 2 r 时，则满足

可得

C 错误， D 正确。

故选 D 。

考点梳理:

根据可圈可点权威老师分析，试题“ ”主要考查你对带电粒子在电场中的加速等考点的理解。关于这些考点的“资料梳理”如下：

◎ 带电粒子在电场中的加速的定义

带电粒子在电场中的直线运动:

(1)如不计重力，电场力就是粒子所受合外力，粒子做直线运动时的要求有：
①对电场的要求：或是匀强电场，或不是匀强电场但电场的电场线有直线形状。
②对初始位置的要求：在匀强电场中任一点开始运动都可以，在非匀强电场中带电粒子的初始位置必须在直线形的电场线上。
③对初速度的要求：初速度或为零，或不为零但与所在的电场线共线。
(2)粒子在电场中做直线运动的处理方法有两种：
①将牛顿第二定律与运动学公式结合求解，这种方法只能用在匀强电场中。不考虑重力时，常用的基本方程有：
等.
②由动能定理求解不涉及时间的问题，这种方法对匀强电场、非匀强电场均适用。不考虑重力时，基本方程为：

需要特别注意的是式中U是质点运动中所经历的始末位置之间的电势差，而不一定等于题目中给定的电压，如带电粒子从电压为U的两板中点运动到某一极板上时，经历的电压仅是

◎ 带电粒子在电场中的加速的知识扩展

1、在匀强电场中的加速问题，一般属于物体受恒力（重力一般不计）作用运动问题。处理的方法有两种：
①根据牛顿第二定律和运动学公式结合求解：，，；
②根据动能定理与电场力做功，运动学公式结合求解：。
2、在非匀强电场中的加速问题，一般属于物体受变力作用运动问题。处理的方法只能根据动能定理与电场力做功，运动学公式结合求解：。