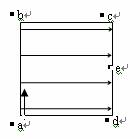
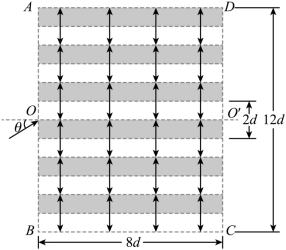
某装置用电场控制带电粒子运动，工作原理如图所示，矩形 区域内存在多层紧邻的匀强电场，每层的高度均为 d ，电场强度大小均为 E ，方向沿竖直方向交替变化， 边长为 ， 边长为 ，质量为 m 、电荷量为 的粒子流从装置左端中点射入电场，粒子初动能为 ，入射角为 ，在纸面内运动，不计重力及粒子间的相互作用力。

（ 1 ）当 时，若粒子能从 边射出，求该粒子通过电场的时间 t ；

（ 2 ）当 时，若粒子从 边射出电场时与轴线 的距离小于 d ，求入射角 的范围；

（ 3 ）当 ，粒子在 为 范围内均匀射入电场，求从 边出射的粒子与入射粒子的数量之比 。

答案

（ 1 ） ；（ 2 ） 或 ；（ 3 ）

【详解】（ 1 ）电场方向竖直向上，粒子所受电场力在竖直方向上，粒子在水平方向上做匀速直线运动，速度分解如图所示

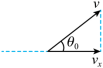
粒子在水平方向的速度为

根据 可知

解得

（ 2 ）粒子进入电场时的初动能

粒子进入电场沿电场方向做减速运动，由牛顿第二定律可得

粒子从 边射出电场时与轴线 的距离小于 d ，则要求

解得

所以入射角的范围为

或

（ 3 ）设粒子入射角为 时，粒子恰好从 D 点射出，由于粒子进入电场时，在水平方向做匀速直线运动，在竖直方向反复做加速相同的减速运动，加速运动。粒子的速度

运动时间为

粒子在沿电场方向，反复做加速大小相同的减速运动，加速运动，则

则

则粒子在分层电场中运动时间相等，设为 ，则

且

代入数据化简可得

即

解得

（舍去）或

解得

则从 边出射的粒子与入射粒子的数量之比