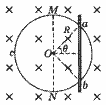
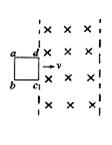
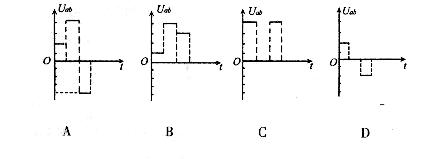
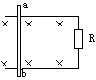
舰载机电磁弹射是现在航母最先进的弹射技术，我国在这一领域已达到世界先进水平。某兴趣小组开展电磁弹射系统的设计研究，如图 1 所示，用于推动模型飞机的动子（图中未画出）与线圈绝缘并固定，线圈带动动子，可在水平导轨上无摩擦滑动。线圈位于导轨间的辐向磁场中，其所在处的磁感应强度大小均为 B 。开关 S 与 1 接通，恒流源与线圈连接，动子从静止开始推动飞机加速，飞机达到起飞速度时与动子脱离；此时 S 掷向 2 接通定值电阻 R ₀ ，同时施加回撤力 F ，在 F 和磁场力作用下，动子恰好返回初始位置停下。若动子从静止开始至返回过程的 v - t 图如图 2 所示，在 t ₁ 至 t ₃ 时间内 F =(800 － 10 v ） N ， t ₃ 时撤去 F 。已知起飞速度 v ₁ =80m/s ， t ₁ =1.5s ，线圈匝数 n =100 匝，每匝周长 l =1m ，飞机的质量 M =10kg ，动子和线圈的总质量 m =5kg ， R ₀ =9.5Ω ， B =0.1T ，不计空气阻力和飞机起飞对动子运动速度的影响，求

（ 1 ）恒流源的电流 I ；

（ 2 ）线圈电阻 R ；

（ 3 ）时刻 t ₃ 。

答案

（ 1 ） 80A ；（ 2 ） ；（ 3 ）

【详解】（ 1 ）由题意可知接通恒流源时安培力

动子和线圈在 0~ t ₁ 时间段内做匀加速直线运动，运动的加速度为

根据牛顿第二定律有

代入数据联立解得

（ 2 ）当 S 掷向 2 接通定值电阻 R ₀ 时，感应电流为

此时安培力为

所以此时根据牛顿第二定律有

由图可知在 至 期间加速度恒定，则有

解得

，

（ 3 ）根据图像可知

故 ；在 0~ t ₂ 时间段内的位移

而根据法拉第电磁感应定律有

电荷量的定义式

可得

从 t ₃ 时刻到最后返回初始位置停下的时间段内通过回路的电荷量，根据动量定理有

联立可得

解得