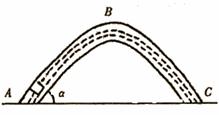
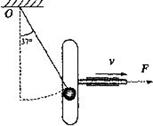
如图所示,在竖直面内,一质量 m 的物块 a 静置于悬点 O 正下方的 A 点,以速度 v 逆时针转动的传送带 MN 与直轨道 AB 、 CD 、 FG 处于同一水平面上, AB 、 MN 、 CD 的长度均为 l 。圆弧形细管道 DE 半径为 R , EF 在竖直直径上, E 点高度为 H 。开始时,与物块 a 相同的物块 b 悬挂于 O 点,并向左拉开一定的高度 h 由静止下摆,细线始终张紧,摆到最低点时恰好与 a 发生弹性正碰。已知 ,
,
,
,
,物块与 MN 、 CD 之间的动摩擦因数
,轨道 AB 和管道 DE 均光滑,物块 a 落到 FG 时不反弹且静止。忽略 M 、 B 和 N 、 C 之间的空隙, CD 与 DE 平滑连接,物块可视为质点,取
。
( 1 )若 ,求 a 、 b 碰撞后瞬时物块 a 的速度
的大小;
( 2 )物块 a 在 DE 最高点时,求管道对物块的作用力 与 h 间满足的关系;
( 3 )若物块 b 释放高度 ,求物块 a 最终静止的位置 x 值的范围(以 A 点为坐标原点,水平向右为正,建立 x 轴)。

答案
( 1 ) ;( 2 )
;( 3 )当
时,
,当
时,
【详解】( 1 )滑块 b 摆到最低点过程中,由机械能守恒定律
解得
与
发生弹性碰撞,根据动量守恒定律和机械能守恒定律可得
联立解得
( 2 )由( 1 )分析可知,物块 与物块
在
发生弹性正碰,速度交换,设物块
刚好可以到达
点,高度为
,根据动能定理可得
解得
以竖直向下为正方向
由动能定理
联立可得
( 3 )当 时,物块位置在
点或
点右侧,根据动能定理得
从 点飞出后,竖直方向
水平方向
根据几何关系可得
联立解得
代入数据解得
当 时,从
释放时,根据动能定理可得
解得
可知物块达到距离 点 0.8m 处静止,滑块 a 由 E 点速度为零,返回到
时,根据动能定理可得
解得
距离 点 0.6m ,综上可知当
时
代入数据得