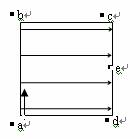
如图为某一径向电场的示意图,电场强度大小可表示为 , a 为常量。比荷相同的两粒子在半径 r 不同的圆轨道运动。不考虑粒子间的相互作用及重力,则( )

A .轨道半径 r 小的粒子角速度一定小
B .电荷量大的粒子的动能一定大
C .粒子的速度大小与轨道半径 r 一定无关
D .当加垂直纸面磁场时,粒子一定做离心运动
答案
BC
【详解】 A .根据电场力提供向心力可得
解得
可知轨道半径 r 小的粒子角速度大,故 A 错误;
BC .根据电场力提供向心力可得
解得
又
联立可得
可知电荷量大的粒子的动能一定大,粒子的速度大小与轨道半径 r 一定无关,故 BC 正确;
D .磁场的方向可能垂直纸面向内也可能垂直纸面向外,所以粒子所受洛伦兹力方向不能确定,粒子可能做离心运动,也可能做近心运动,故 D 错误。
故选 BC 。

 等.
等.