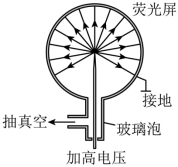
衍射现象限制了光学显微镜的分辨本领,最好的光学显微镜也只能分辨 200nm 大小的物体,而场致发射显微镜的分辨率大大提高。其原理如图所示,在真空玻璃泡中心放置待测金属针(这根金属针的针尖即是该显微镜的观察对象),泡的内壁涂有荧光导电膜,在金属针和荧光导电间加很高的电压,形成如图所示的辐射状的电场。在泡内充以少量氦气,氦原子碰到针尖时会失去一个电子形成氦离子,然后向荧光屏运动,引起荧光材料发光,在荧光屏上就看到了针尖的某种像,如分辨率足够高,还可以分辨出针尖端个别原子的位置。若把氦离子改成电子,并将电极方向互换,打到荧光屏上分辨率会降低。忽略氦离子和电子的重力,其初速度可视为零,不考虑运动过程中带电粒子间相互作用,下列说法中正确的是( )
A .氦离子运动过程中加速度不断增大
B .氦离子运动过程中电势能不断增大
C .分辨率降低是因为电子的德布罗意波长比氦离子的长
D .若所加电压为 U ,玻璃泡的半径为 r ,则距离针尖 处的电场强度大小为
答案
C
【详解】 A .由图发现,越远离针尖,电场线越稀疏,则电场强度越小,则电场力越小,则氦离子运动过程中加速度不断减小,故 A 错误;
B .氦离子由针尖向荧光屏运动过程,运动方向与电场方向一致,电场力做正功,电势能减小,故 B 错误;
C .加速过程,根据动能定理
动量
故到达荧光屏时,电子的动量较小,根据 ,则电子的德布罗意波较长,波动性较明显,导致分辨率低,故 C 正确;
D .泡内上部产生的辐射电场可以看作是针尖处的点电荷产生的电场,根据 可知,某处场强与距离针尖的距离不成反比,故距离针尖
处的电场强度大小不是
,故 D 错误。
故选 C 。

 等.
等.