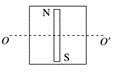
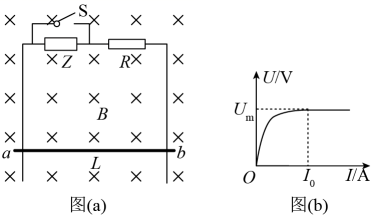
如图（ a ）所示，两根不计电阻、间距为 L 的足够长平行光滑金属导轨，竖直固定在匀强磁场中，磁场方向垂直于导轨平面向里，磁感应强度大小为 B 。导轨上端串联非线性电子元件 Z 和阻值为 R 的电阻。元件 Z 的 图像如图（ b ）所示，当流过元件 Z 的电流大于或等于 时，电压稳定为 U _m 。质量为 m 、不计电阻的金属棒可沿导轨运动，运动中金属棒始终水平且与导轨保持良好接触。忽略空气阻力及回路中的电流对原磁场的影响，重力加速度大小为 g 。为了方便计算，取 ， 。以下计算结果只能选用 m 、 g 、 B 、 L 、 R 表示。

（ 1 ）闭合开关 S 。，由静止释放金属棒，求金属棒下落的最大速度 v ₁ ；

（ 2 ）断开开关 S ，由静止释放金属棒，求金属棒下落的最大速度 v ₂ ；

（ 3 ）先闭合开关 S ，由静止释放金属棒，金属棒达到最大速度后，再断开开关 S 。忽略回路中电流突变的时间，求 S 断开瞬间金属棒的加速度大小 a 。

答案

（ 1 ） ；（ 2 ） ；（ 3 ）

【分析】

【 关键能力 】 本题考 查法拉第电磁感应定律、闭合电路欧姆定律等知识，意在考查考生综合电磁学知识以及力学规律处理问题的能力。

【 压轴题透析 】 3 第（ 1 ）问通过对金属棒的受力分析以及运动分析，求出当金属棒的加速度为零时的最大速度；第（ 2 ）问首先应分析比较第（ 1 ）问中的电流与图（ b ）中 Z 元件的电压达到最大时的电流大小关系，然后通过定值电阻表示出回路中的最大电流，进而求出金属棒的最大速度；第（ 3 ）问的关键在于求出开关断开瞬间回路中的电流，得出导体棒所受的安培力大小，再根据牛顿第二定律求出金属棒的加速度。

【详解】

（ 1 ）闭合开关 S ，金属棒下落的过程中受竖直向下的重力、竖直向上的安培力作用，当重力与安培力大小相等时，金属棒的加速度为零，速度最大，则

由法拉第电磁感应定律得

由欧姆定律得

解得

（ 2 ）由第（ 1 ）问得

由于

断开开关 S 后，当金属棒的速度达到最大时，元件 Z 两端的电压恒为

此时定值电阻两端的电压为

回路中的电流为

又由欧姆定律得

解得

（ 3 ）开关 S 闭合，当金属棒的速度最大时，金属棒产生的感应电动势为

断开开关 S 的瞬间，元件 Z 两端的电压为

则定值电阻两端的电压为

电路中的电流为

金属棒受到的安培力为

对金属棒由牛顿第二定律得

解得

‍