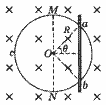
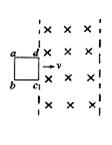
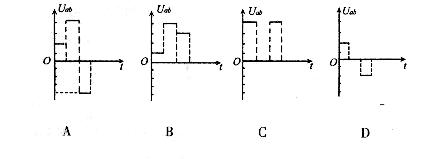
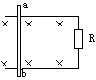
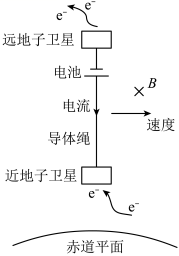
迷你系绳卫星在地球赤道正上方的电离层中，沿圆形轨道绕地飞行。系绳卫星由两子卫星组成，它们之间的导体绳沿地球半径方向，如图所示。在电池和感应电动势的共同作用下，导体绳中形成指向地心的电流，等效总电阻为 r 。导体绳所受的安培力克服大小为 f 的环境阻力，可使卫星保持在原轨道上。已知卫生离地平均高度为 H ，导体绳长为 ，地球半径为 R ，质量为 M ，轨道处磁感应强度大小为 B ，方向垂直于赤道平面。忽略地球自转的影响。据此可得，电池电动势为（　　）

A ． B ．

C ． D ．

答案

A

【详解】

根据

可得卫星做圆周运动的线速度

根据右手定则可知，导体绳产生的感应电动势相当于上端为正极的电源，其大小为

因导线绳所受阻力 f 与安培力 F 平衡，则安培力与速度方向相同，可知导线绳中的电流方向向下，即电池电动势大于导线绳切割磁感线产生的电动势 ，可得

解得

故选 A 。