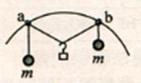
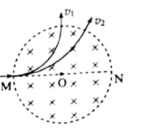
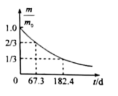
如图 ,距离为 d 的两平行金属板 P、Q 之间有一匀强磁场,磁感应强度大小为B1,束遠度大小为v的等离子体垂直于磁场喷入板间。相距为 L 的两光滑平行金属导轨固定在与导轨平面垂直的匀强磁场中,磁感应强度大小为B2导轨平面与水平面夹角为θ,两导轨分别与 P、Q 相连。质量为 m、电阻为 R 的金属棒 ab 垂直导轨放置,恰好静止。重力加速度为 g,不计导轨电阻、板间电阻和等离子体中的粒子重力,下列说法正确的是
A.导轨处磁场得方向垂直导轨平面向上,
B.导轨处磁场得方向垂直导轨平面向下,
C.导轨处磁场得方向垂直导轨平面向上,
D.导轨处磁场得方向垂直导轨平面向下,
答案
B
【分析】此题为磁流体发电机模型,等离子体进入磁场后,正负离子受到洛伦兹力发生偏转,依据左手定则判断正负离子的偏转方向,得到金属板 P、Q的带电性质,得到金属棒ab中电流方向;金属棒ab恰好静止,由受力平衡条件判断出所受安培力的方向并求出电流大小,再依据左手定则判断出导轨处磁场的方向;等离子体的正负离子在磁场B 1 中受到电场力与洛伦兹力,稳定后此二力平衡,由闭合电路欧姆定律求出平行金属板 P、Q之间的电压,由 求出板间电场强度,由等离子体受到电场力等于洛伦兹力,求出等离子体的速度大小。
【解答】解:平行金属板 P、Q之间磁感应强度方向由N极指向S极,由左手定则判断,等离子体中的正离子向金属板Q偏转,负离子向金属板P偏转,可知金属板Q带正电荷(电源正极),金属板P带负电荷(电源负极),金属棒ab中电流方向由a流向b,已知磁场B 2 的方向垂直导轨平面,由左手定则可知,金属棒 ab所受安培力平行于导轨平面向上或者向下,金属棒ab处于静止,由受力平衡条件判断其所受安培力沿导轨平面向上,再由左手定则判断出导轨处磁场的方向垂直导轨平面向下。
金属棒 ab恰好静止,由受力平衡可得:B 2 IL=mgsinθ,
由闭合电路欧姆定律可得,平行金属板 P、Q之间的电压U=IR,
金属板 P、Q之间电场强度
等离子体的正负离子在磁场 B 1 中受到电场力与洛伦兹力,稳定后此二力平衡,则 qvB 1 =qE,联立解得 ![]() ,故 B正确,ACD错误。
,故 B正确,ACD错误。
故选: B。