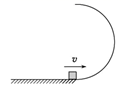
如图,半圆形光滑轨道固定在水平地面上,半圆的直径与地面垂直,一小物块以速度v从轨道下端滑入轨道,并从轨道上端水平飞出,小物块落地点到轨道下端的距离与轨道半径有关,此距离最大时,对应的轨道半径为(重力加速度为g)( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
答案
B
【分析】
根据动能定理得出物块到达最高点的速度,结合高度求出平抛运动的时间,从而得出水平位移的表达式,结合表达式,运用二次函数求极值的方法得出距离最大时对应的轨道半径.
【详解】
设半圆的半径为R,根据动能定理得:−mg•2R=![]() mv′2−
mv′2−![]() mv2,离开最高点做平抛运动,有:2R=
mv2,离开最高点做平抛运动,有:2R=![]() gt2,x=v′t,联立解得:
gt2,x=v′t,联立解得: ,可知当R=
,可知当R=![]() 时,水平位移最大,故B正确,ACD错误.故选B.
时,水平位移最大,故B正确,ACD错误.故选B.
【点睛】
本题考查了动能定理与圆周运动和平抛运动的综合运用,得出水平位移的表达式是解决本题的关键,本题对数学能力的要求较高,需加强这方面的训练.