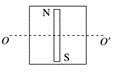
如图所示，在正方形线圈的内部有一条形磁铁，线圈与磁铁在同一平面内，两者有共同的中心轴线OO′，关于线圈中产生感应电流的下列说法中，正确的是( )
A．当磁铁向纸面外平移时，线圈中产生感应电流
B．当磁铁向上平移时，线圈中产生感应电流
C．当磁铁向下平移时，线圈中产生感应电流
D．当磁铁N极向纸外，S极向纸里绕OO′轴转动时，线圈中产生感应电流
D
【解析】
使磁铁沿垂直于线圈平面的方向向纸外平动时，穿过线圈的磁通量仍为零，不变，不产生感应电流．故A错误．当磁铁向上平移时，线圈磁通量保持为零，不变，不产生感应电流．故B错误；当磁铁向下平移时，线圈磁通量保持为零，不变，不产生感应电流．故C错误．图示时刻穿过正方形线圈的磁通量为零，当N极向纸外，S极向纸里绕
轴转动时，线圈的磁通量增大，则线圈中产生感应电流．故D正确．故选D．
【点睛】根据产生感应电流的条件：穿过正方形线圈圈的磁通量要发生变化来判断．图示时刻穿过正方形线圈的磁通量为零．
知识扩展：
关于“切割”的讨论：
闭合电路的一部分导体做切割磁感线运动时．闭合电路中产生感应电流。如图所示，当导体 AD向右运动时，穿过ABCD的磁通量发生变化(面积变大)，所以ABCD回路中产生感应电流。由此可见部分导体“切割磁感线产生感应电流”和“磁通量变化”在本质上是一致的。
在利用“切割”来讨论和判断有无感应电流时，应该注意： 
(1)导体是否将磁感线“割断”，如果没有“割断”，就不能说切割。如图所示，甲、乙两图中，导线是真“切割”：而图丙中，线圈与磁感线平行，线圈没有切割磁感线。 
(2)即使导体真“切割”了磁感线，也不能保证就能产生感应电流。如图所示，对于图甲，尽管导线框 “切割”了磁感线(匀强磁场)，但此时穿过闭合线框的磁通量并没有发生变化，没有感应电流；对于图乙，导线框的一部分“切割”了磁感线，穿过线框的磁感线条数越来越少，线框中有感应电流；对于图丙，闭合导线框在非匀强磁场中运动，切割了磁感线，同时穿过线框的磁感线条数减少，线框中有感应电流： 
(3)即使是闭合回路的部分导体做切割磁感线的运动，也不能绝对保证一定存在感应电流，如图所示，ABCD 导线框的一部分在匀强磁场中上下平动，尽管是部分切割，但同样在线框中没有感应电流，由以上讨论可见，导体切割磁感线，不是在导体中产生感应电流的充要条件．归根结底还要看穿过闭合回路的磁通量是否发生变化。
超导体的电磁感应现象：
无论是磁场变化还是导体与磁场间相对运动引起的电磁感应现象，对普通导体来说，非静电力都是自由电荷定向移动的动力，能量转化是单向的，楞次定律和右手定则都是在非静电力是动力的基础上提出的。对于超导体来说，如果超导体内原来无电流，可用楞次定律或右手定则来判定超导体内产生的感应电流的方向，只是当磁通量持续增加或是持续减小时，超导体内的感应电流总是增大的，磁通量停止变化时，超导体内的感应电流保持恒定，当磁通量的变化方向改变时，非静电力成为超导体内自由电荷定向运动的阻力．此时用楞次定律或右手定则得到的方向与实际电流的方向相反。
事实上，楞次定律或右手定则确定的是电磁感应中正电荷所受非静电力的方向，在用来判定超导体中感应电流时，要先判定非静电力是自由电荷定向运动的动力还是阻力，进而再判定感应电流的大小、方向。
登录并加入会员可无限制查看知识点解析
