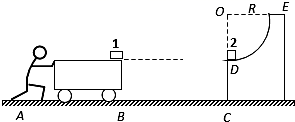
如图所示，一辆质量为M的小车静止在水平面上，车面上右端点有一可视为质点的滑块1，水平面上有与车右端相距为4R的固定的
光滑圆弧轨道，其圆周半径为R，圆周E处的切线是竖直的，车上表面与地面平行且与圆弧轨道的末端D等高，在圆弧轨道的最低点D处，有另一个可视为质点的滑块2，两滑块质量均为m．某人由静止开始推车，当车与圆弧轨道的竖直壁CD碰撞后人即撤去推力并离开小车，车碰后靠着竖直壁静止但不粘连，滑块1和滑块2则发生碰撞，碰后两滑块牢牢粘在一起不再分离．车与地面的摩擦不计，滑块1、2与车面的摩擦系数均为μ，重力加速度为g，滑块与车面的最大静摩擦力可认为等于滑动摩擦力．
（1）若人推车的力是水平方向且大小为
，则在人推车的过程中，滑块1与车是否会发生相对运动？
（2）在（1）的条件下，滑块1与滑块2碰前瞬间，滑块1的速度多大？
（3）若车面的长度为
，小车质量M=km，则k的取值在什么范围内，两个滑块最终没有滑离车面？
答案
（1）滑块1与车面之间没有发生相对滑动；（2）
；（3）k≤2
【详解】
（1）设滑块1与车不发生相对滑动，加速度大小为a，由牛顿第二定律有：F=（M+m）a
此时滑块受到的静摩擦力大小为：f=ma
而：
联立解得：
又滑块1与车面的最大静摩擦力为：fm=μmg
显然f＜fm，说明滑块1与车面之间没有发生相对滑动．
（2）设滑块1与滑块2碰撞前瞬间滑块1的速度为v，根据动能定理有：
联立求得：
（3）设滑块1和2发生碰撞后的共同速度为v1，由动量守恒定律有：mv=2mv1
联立求得：
两滑块粘合在一起后以v1的速度冲上光滑圆弧轨道，由于圆弧轨道的E处的切线是竖直的，则无论两滑块在圆弧轨道上运动，还是从E处竖直向上离开圆弧轨道，最后还是沿着圆弧轨道回到D处，整个过程中两滑块的机械能守恒，两滑块最终以速度v1冲上车面．设两滑块滑到车的左端时，若滑块刚好不滑出车面，滑块和车应有共同的速度设为v2，由系统的动量守恒有：2mv1=（2m+km）v2，
由系统的能量守恒，有：
联立解得：k=2
所以当k≤2时，两个滑块最终没有滑离小车．
