如图所示为一皮带传动装置,右轮半径为r,a点在它的边缘上;左轮半径为2r,b点在它的边缘上.若在传动过程中皮带不打滑,则a点与b点的向心加速度大小之比( )
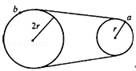
A.aa:ab=4:1 B.aa:ab=1:4
C.aa:ab=2:1 D.aa:ab=1:2
答案
C
【解析】
试题分析:该图所示为皮带传送装置,所以A.b两点线速度相等![]() ,由向心加速度
,由向心加速度![]() ,可求出A.b两点向心加速度之比为2:1,C正确。
,可求出A.b两点向心加速度之比为2:1,C正确。
考点:皮带传动、向心加速度
如图所示为一皮带传动装置,右轮半径为r,a点在它的边缘上;左轮半径为2r,b点在它的边缘上.若在传动过程中皮带不打滑,则a点与b点的向心加速度大小之比( )

A.aa:ab=4:1 B.aa:ab=1:4
C.aa:ab=2:1 D.aa:ab=1:2
C
【解析】
试题分析:该图所示为皮带传送装置,所以A.b两点线速度相等![]() ,由向心加速度
,由向心加速度![]() ,可求出A.b两点向心加速度之比为2:1,C正确。
,可求出A.b两点向心加速度之比为2:1,C正确。
考点:皮带传动、向心加速度
向心力的定义:
在圆周运动中产生向心加速度的力。![]() 。
。


 (当时
(当时 ,绳子对球产生拉力)
,绳子对球产生拉力) (实际上小球还没有到最高点时,就脱离了轨道)
(实际上小球还没有到最高点时,就脱离了轨道)
 (N为支持力)
(N为支持力) ,有
,有 (N为支持力)
(N为支持力) ,有
,有 (N=0)
(N=0) ,有
,有 (N为拉力)
(N为拉力)向心力的特性:
1、向心力
总是指向圆心,产生向心加速度,向心力只改变线速度的方向,不改变速度的大小,大小![]() ,方向总是指向圆心(与线速度方向垂直),方向时刻在变化,是一个变力。向心力可以由某个具体力提供,也可以由合力提供,还可以由分力提供。
,方向总是指向圆心(与线速度方向垂直),方向时刻在变化,是一个变力。向心力可以由某个具体力提供,也可以由合力提供,还可以由分力提供。
2、轻绳模型
Ⅰ、轻绳模型的特点:
①轻绳的质量和重力不计;
②可以任意弯曲,伸长形变不计,只能产生和承受沿绳方向的拉力;
③轻绳拉力的变化不需要时间,具有突变性。
Ⅱ、轻绳模型在圆周运动中的应用
小球在绳的拉力作用下在竖直平面内做圆周运动的临界问题:
①临界条件:小球通过最高点,绳子对小球刚好没有力的作用,由重力提供向心力:
②小球能通过最高点的条件: (当时
(当时 ,绳子对球产生拉力)
,绳子对球产生拉力)
③不能通过最高点的条件: (实际上小球还没有到最高点时,就脱离了轨道)
(实际上小球还没有到最高点时,就脱离了轨道)
3、轻杆模型:
Ⅰ、轻杆模型的特点:
①轻杆的质量和重力不计;
②任意方向的形变不计,只能产生和承受各方向的拉力和压力;
③轻杆拉力和压力的变化不需要时间,具有突变性。
Ⅱ、轻杆模型在圆周运动中的应用
轻杆的一端连着一个小球在竖直平面内做圆周运动,小球通过最高点时,轻杆对小球产生弹力的情况:
①小球能通过最高点的临界条件: (N为支持力)
(N为支持力)
②当时 ,有
,有 (N为支持力)
(N为支持力)
③当时 ,有
,有 (N=0)
(N=0)
④当时 ,有
,有 (N为拉力)
(N为拉力)
知识点拨:
向心力是从力的作用效果来命名的,因为它产生指向圆心的加速度,所以称它为向心力。它不是具有确定性质的某种类型的力。相反,任何性质的力都可以作为向心力。实际上它可是某种性质的一个力,或某个力的分力,还可以是几个不同性质的力沿着半径指向圆心的合外力。对一个物体进行受力分析的时候,是不需要画向心力的,向心力是效果力。
登录并加入会员可无限制查看知识点解析
有一个惊险的杂技节目叫“飞车走壁”,杂技演员骑摩托车先在如图2所示的大型圆筒底部作速度较小半径较小的圆周运动,通过逐步加速,圆周运动半径亦逐步增大,最后能以较大的速度在垂直的壁上作匀速圆周运动,这时使车子和人整体作圆周运动的向心力是( )
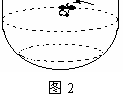 |
C.摩托车本身的动力 D.重力和摩擦力的合力