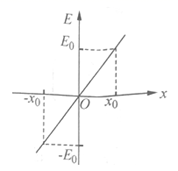
空间存在某静电场,在x轴上各点的场强E随坐标x的分布规律如图所示,规定x轴的正方向为电场强度E的正方向.一个带电粒子在x轴上以x=0点为对称中心做往复运动.已知粒子仅受电场力作用,运动中电势能和动能的总和为A,且x=0处,电势为零.则
A.该粒子一定带负电
B.该粒子在x=0点两侧分别做匀变速直线运动
C.x=x0处的电势为![]()
D.若该粒子带电量的绝对值为q,则粒子运动区间为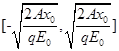
答案
ACD
【详解】
由图像可知在O点右侧的电场线水平向右,在O点左侧的电场线水平向左,假设粒子带正电,则粒子在O点右侧向右运动时一直做加速运动因此不会做往复运动,因此粒子不可能带正电,当粒子带负电时向右侧运动时做减速运动,减速到零反向加速过O点后继续减速运动,做的时往复运动,因此粒子带负电,A正确;
由图像可知该电场不是匀强电场,粒子的受力会发生变化,因此不做匀变速直线运动,B错误;
![]() 图像的面积为电势差,沿着电场线方向电势降低,因此
图像的面积为电势差,沿着电场线方向电势降低,因此![]() 得,
得,![]() C正确;
C正确;
粒子的总能量为A,且O点的电势能为零,则O点的动能为A,粒子向x轴正向运动的最远距离时速度为零,能量转化为该点的电势能,由能量守恒可知![]() 得
得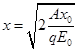 ,故D正确.
,故D正确.


 计算,此公式只适用于匀强电场中,可变形为
计算,此公式只适用于匀强电场中,可变形为 式中x为电荷初、末位置在场强方向上的位移。
式中x为电荷初、末位置在场强方向上的位移。  计算,对任何电场都适用。对于
计算,对任何电场都适用。对于 的符号有两种处理方法:
的符号有两种处理方法:  的绝对值代入
的绝对值代入 时,
时, ;否则
;否则
 。其中
。其中
 ,对任何电场都适用。
,对任何电场都适用。  。此方法对任何电场、任何形式的运动都适用。
。此方法对任何电场、任何形式的运动都适用。 ,得
,得 ,即电场力的大小等于电荷本身所带电荷量与所在处场强的乘积。
,即电场力的大小等于电荷本身所带电荷量与所在处场强的乘积。  A. 两处的电场方向相同,E1>E2
A. 两处的电场方向相同,E1>E2