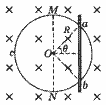
如图所示，粗细均匀的电阻为r的金属圆环，放在图示的匀强磁场中，磁感强度为B，圆环直径为l，另一长为l，电阻为r/2的金属棒ab放在圆环上，接触电阻不计．当ab棒以 v0向左运动到图示虚线位置时，金属棒两端电势差为（ ）
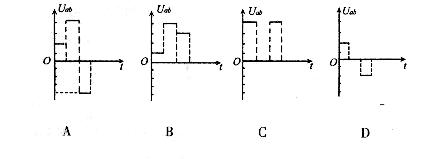
A．Blv0 B．
C．
D．
C
【解析】
当ab棒以
向左运动到图示虚线位置时产生的感应电动势为：
，
外电路总电阻为：
金属棒两端的电势差是外电压，由欧姆定律得金属棒两端电势差为：
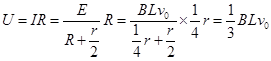
A．Blv0，与结论不相符，选项A错误；
B．
，与结论不相符，选项B错误；
C．
，与结论相符，选项C正确；
D．
，与结论不相符，选项D错误；
故选C．
点睛：金属棒向左运动，切割磁感线产生感应电流，相当于电源，由 求出感应电动势，由并联电路特点求出外电路电阻，然后应用欧姆定律求出金属棒两端电势差．
法拉第电磁感应定律：
（n为线圈匝数）。 
； 
。 导体切割磁感线的两个特例：
的区别与联系及选用原则：
电磁感应中动力学问题的解法：
电磁感应和力学问题的综合，其联系的桥梁是磁场对感应电流的安培力，因为感应电流与导体运动的加速度有相互制约的关系。
1．分析思路
(1)用法拉第电磁感应定律和楞次定律求感应电动势的大小和方向。
(2)求回路中的电流。
(3)分析研究导体受力情况(包含安培力，用左手定则确定其方向)。
(4)列动力学方程或平衡方程求解。
2．常见的动态分析这类问题中的导体一般不是做匀变速运动，而是经历一个动态变化过程再趋于一个稳定状态，故解这类问题时正确进行动态分析确定最终状态是解题的关键。同时也要抓好受力情况和运动情况的动态分析，研究顺序为：导体受力运动产生感应电动势一感应电流一通电导体受安培力一合外力变化一加速度变化一速度变化一周而复始地循环，循环结束时，加速度等于零．导体达到稳定运动状态。
电磁感应中的动力学临界问题：
(1)解决这类问题的关键是通过运动状态的分析，寻找过程中的临界状态，如速度、加速度求最大值或最小值的条件。
(2)基本思路：
登录并加入会员可无限制查看知识点解析
bcd
