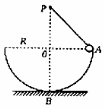
如图所示，一光滑半圆形轨道固定在水平地面上，圆心为O、半径为R，一根轻橡皮筋一端连在可视为质点的小球上。另一端连在距离O点正上方R处的P点。小球放在与O点等高的轨道上A点时，轻橡皮筋处于原长。现将小球从A点由静止释放，小球沿圆轨道向下运动，通过最低点B时对圆轨道的压力恰好为零。已知小球的质量为m，重力加速度为g，则小球从A点运动到B点的过程中下列说法正确的是（ ）
A．小球通过最低点时，橡皮筋的弹力等于mg
B．橡皮筋弹力做功的功率逐渐变大
C．小球运动过程中，橡皮筋弹力所做的功等于小球动能增加量
D．小球运动过程中，机械能的减少量等于橡皮筋弹性势能的增加量
答案
D
【解析】
小球运动到最低点时，根据牛顿第二定律可得F-mg=m
，橡皮筋的弹力F=mg+m，故F大于mg，故A错误；根据P=Fvcosα可知，开始时v=0，则橡皮筋弹力做功的功率P=0．在最低点速度方向与F方向垂直，α=90°，则橡皮筋弹力做功的功率P=0，故橡皮筋弹力做功的功率先变大后变小，故B错误；小球运动过程中，根据动能定理知，重力做功和橡皮筋弹力所做的功之和等于小球动能增加量，故C错误。小球和弹簧组成的系统机械能守恒，知小球运动过程中，机械能的减少量等于橡皮筋弹性势能的增加量，故D正确。
