如图所示,质量可忽略的绝缘细杆做成正方体框架,边长为a,框架的每个顶点固定着一个带电荷量为+q,质量为m的小球,将这个框架静止放在足够粗糙的水平面上,水平面上方有水平向右的匀强电场,场强为E,下列说法正确的是
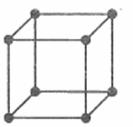
A.立方体中心位置处电场强度为零
B.上方四个小球受到的电场力的合力均相同
C.若以右下底边为轴把这个立方体向右侧翻转90°,系统电势能减少了6qEa
D.若以右下底边为轴把这个立方体向右侧翻转90°,系统电势能减少了8qEa
答案
D
【解析】
A.根据对称性可知,八个带正电的小球在立方体中心位置处产生的合电场强度为零,则此位置处的场强只等于匀强电场的场强E,选项A错误;
B.上方的右边两个小球受到的电场力的合力相同,上方的左边两个小球受到的电场力的合力相同,但是与右边两个小球受到的电场力不同,选项B错误;
CD.若以右下底边为轴把这个立方体向右侧翻转90°,则电场力对右上方两球做功为2qEa;对左上方两个球做功2qE∙2a;对左下方两球做功2qEa;,则共做功为8qEa,即系统电势能减少了8qEa,选项D正确,C错误;
故选D。


 计算,此公式只适用于匀强电场中,可变形为
计算,此公式只适用于匀强电场中,可变形为 式中x为电荷初、末位置在场强方向上的位移。
式中x为电荷初、末位置在场强方向上的位移。  计算,对任何电场都适用。对于
计算,对任何电场都适用。对于 的符号有两种处理方法:
的符号有两种处理方法:  的绝对值代入
的绝对值代入 时,
时, ;否则
;否则
 。其中
。其中
 ,对任何电场都适用。
,对任何电场都适用。  。此方法对任何电场、任何形式的运动都适用。
。此方法对任何电场、任何形式的运动都适用。 ,得
,得 ,即电场力的大小等于电荷本身所带电荷量与所在处场强的乘积。
,即电场力的大小等于电荷本身所带电荷量与所在处场强的乘积。  A. 两处的电场方向相同,E1>E2
A. 两处的电场方向相同,E1>E2