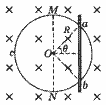
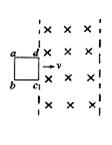
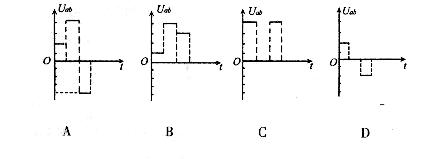
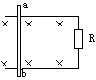
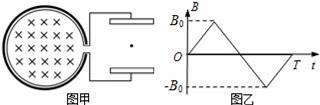
如图甲所示,圆形的刚性金属线圈与一平行板电容器连接,线圈内存在垂直于线圈平面的匀强磁场,磁感应强度B随时间变化的关系如图乙所示(以图示方向为正方向).t=0时刻,平行板电容器间一带正电的粒子(重力可忽略不计)由静止释放,假设粒子运动未碰到极板,不计线圈内部磁场变化对外部空间的影响,下列粒子在板间运动的速度图象和位移图象(以向上为正方向)中,正确的是( )

A.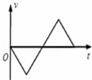
 B.
B.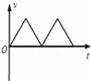
 C.
C.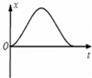
 D.
D.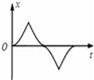

答案
解:AB、0~![]()
![]() 内情况:由楞次定律可知,金属板上极板带负电,金属板下极板带正电;
内情况:由楞次定律可知,金属板上极板带负电,金属板下极板带正电;
因粒子带正电,则粒子所受电场力方向竖直向上而向上做匀加速运动.
![]()
![]() ~
~![]()
![]() 内情况:由楞次定律可知,金属板上极板带正电,金属板下极板带负电;
内情况:由楞次定律可知,金属板上极板带正电,金属板下极板带负电;
因粒子带正电,则粒子所受电场力方向竖直向下而向上做匀减速运动,直到速度为零.
![]()
![]() ~
~![]()
![]() 内情况:由楞次定律可知,金属板上极板带正电,金属板下极板带负电,带正电粒子向下匀加速,
内情况:由楞次定律可知,金属板上极板带正电,金属板下极板带负电,带正电粒子向下匀加速,
同理,![]()
![]() ~T内情况:由楞次定律可知,金属板上极板带负电,金属板下极板带正电;
~T内情况:由楞次定律可知,金属板上极板带负电,金属板下极板带正电;
因粒子带正电,则粒子所受电场力方向竖直向上,而向下做匀减速运动,直到速度为零.故AB错误;
CD、由A选项分析可知,![]()
![]() 末速度减小为零,位移最大,当T末,粒子回到了原来位置.故C正确,D错误;
末速度减小为零,位移最大,当T末,粒子回到了原来位置.故C正确,D错误;
故选:C.





 的区别与联系及选用原则:
的区别与联系及选用原则: