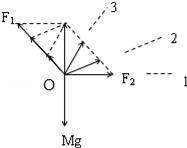
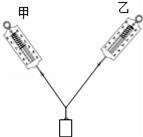
如图所示，在竖直平面内，用甲、乙两个弹簧秤通过细线拉着一个钩码，使之处于静止状态．若保持甲弹簧秤拉力的方向不变，缓慢地调节乙弹簧秤，使两细线之间的夹角增大一些，则（ ）
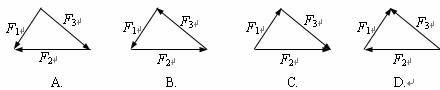
A．两拉力的合力可能增大 B．两拉力的合力可能减小
C．甲弹簧秤的示数可能减小 D．乙弹簧秤的示数可能减小
解：由平衡条件得知，甲、乙两个拉力F1和F2的合力与重力G大小相等、方向相反，保持不变，作出甲、乙两个在三个不同位置时力的合成图，
如图，在甲、乙从1→2→3三个位置的过程中，可以看出，当甲、乙两个方向相互垂直时，F2最小，可见，F1逐渐减小，F2先逐渐减小后逐渐增大．
甲的拉力逐渐减小，乙的拉力先减小后增大．
故选：D
。 力的运算法则:
1．平行四边形定则
作用在同一点的两个互成角度的力的合力，不等于两分力的代数和，而是遵循平行四边形定则。如果以表示两个共点力F1和F2的线段为邻边作平行四边形，那么合力F的大小和方向就可以用这两个邻边之间的对角线表示，这叫做力的平行四边形定则，如图所示。 
2．三角形定则和多边形定则如图(a)所示，两力F1、F2合成为F的平行四边形定则，可演变为(b)图，我们将(b)图称为三角形定则合成图，即将两分力F1、F2首尾相接，则F就是由F，的尾端指向F2的首端的有向线段所表示的力。
如果是多个力合成，则由三角形定则合成推广可得到多边形定则，如图为三个力F1，F2、F3的合成图，F 为其合力。
登录并加入会员可无限制查看知识点解析
