如图所示，圆弧线a、b、c代表某固定点电荷电场中的三个等势面，相邻两等势面间的距离相等，直线是电场中的几条没标明方向的电场线，粗曲线是一带正电粒子只在电场力作用下运动轨迹的一部分，M、N是轨迹上的两点．粒子过M、N两点的加速度大小分别是aM、aN，电势能分别是EPM、EPN，a、b、c的电势分别是φa、φb、φc，ab间，bc间的电势差分别是Uab、Ubc，则下列判断中正确的是（ ）
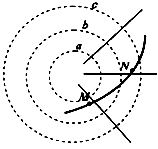
A．aM＞aN，EPM＞EPN B．φa＜φb＜φc，EPM＜EPN
C．aM＞aN，Uab=Ubc D．Uab=Ubc，EPM＜EPN
答案
解：根据运动轨迹可知电场力指向运动轨迹的内侧即斜向左上方，由于质点带正电，因此电场线方向也指向左上方，所以正电荷受到点电荷的吸引力，所以圆心处的点电荷一定带负电，电场线的方向指向圆心，所以φa＜φb＜φc，
根据点电荷的电场线的分布特点可得，M点的电场线密，所以正电荷在M点受到的电场力大，产生的加速度大，即：aM＞aN；
根据点电荷的电场线的分布特点可得，ab之间的电场强度大于bc之间的电场强度，由于相邻两等势面间的距离相等，根据U=Ed可得，Uab＞Ubc；
设粒子从M向N运动，正电荷受到的电场力的方向指向圆心，所以受力的方向与M到N的方向之间的夹角是钝角，电场力做功负功，电势能减小，所以EPM＜EPN．只有选项B正确．
故选：B
的正负，再由
比较
的大小。若
，则
；则
