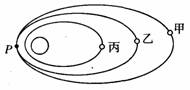
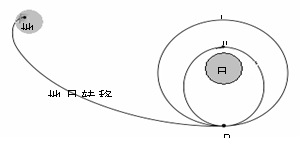
2013年12月2日，嫦娥三号探测器顺利发射。嫦娥三号要求一次性进入近地点210公里、远地点约36.8万公里的地月转移轨道。12月10日晚上九点二十分，在太空飞行了九天的“嫦娥三号”飞船，再次成功变轨，从100km×100k
m的环月圆轨道Ⅰ，降低到近月点15km、远月点100km的椭圆轨道Ⅱ，两轨道相交于点P，如图所示。若绕月运行时只考虑月球引力作用，关于“嫦娥三号”飞船，以下说法正确的是
A．在轨道Ⅰ上运动的周期小于在轨道Ⅱ上运动的周期
B．沿
轨道I运行至P点的速度等于沿轨道II运行至P点的速度
C．沿轨道I运行至P点的加速度等于沿轨道II运行至P点的加速度
D．在轨道Ⅰ上的势能与动能之和比在轨道Ⅱ上的势能与动能之和大
答案
CD
【解析】
试题分析：根据开普勒行星运动第三定律
可知，在轨道Ⅰ的半径大于在轨道Ⅱ的半长轴，故在轨道Ⅰ上运动的周期大于在轨道Ⅱ上运动的周期，选项A错误；沿轨道I运行至P点时要通过减速才能进入轨道II，沿轨道I运行至P点的速度大于沿轨道II运行至P点的速度，选项B错误；在轨道I上的P点和轨道II上的P点所受的万有引力相
同，故沿轨道I运行至P点的加速度等于沿轨道II运行至P点的加速度，选项C正确；在轨道Ⅰ上的势能与动能之和比在轨道Ⅱ上的势能与动能之和大，选项D正确；故选CD.
考点：开普勒行星运动定律；万有引力定律。
