如图(a)所示,A、B为钉在光滑水平面上的两根铁钉,小球C用细绳拴在铁钉B上(细绳能承受足够大的拉力),A、B、C在同一直线上。t=0时,给小球一个垂直于绳的速度,使小球绕着两根铁钉在水平面上做圆周运动。在0≤t≤10s时间内,细绳的拉力随时间变化的规律如图(b)所示,则下列说法中正确的有( )
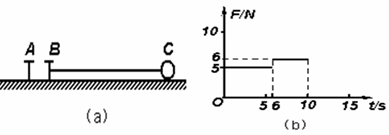
A.两钉子间的距离为绳长的1/6
B.t=10.5s时细绳拉力的大小为6N
C.t=14s时细绳拉力的![]() 大小为10N
大小为10N
D.细绳第三次碰钉子到第四次碰钉子的时间间隔为3s
答案
ABD
【解析】
试题分析:0~6s内绳子的拉力不变,知F1=m![]() ,6~10s内拉力大小不变,知F2=m
,6~10s内拉力大小不变,知F2=m![]() ,因为F2=
,因为F2=![]()
F1,则l′=![]() l,两钉子之间的间距△x=l−
l,两钉子之间的间距△x=l−![]() l=
l=![]() l.故A正确.第一个半圈经历的时间为6s,则
l.故A正确.第一个半圈经历的时间为6s,则![]() =6s,则第二个半圈的时间t′=
=6s,则第二个半圈的时间t′=![]() =
=![]() t=5s,则t=10.5s时,小球在转第二个半圈,则绳子的拉力为6N.故B正确.小球转第三个半圈的时间t″=
t=5s,则t=10.5s时,小球在转第二个半圈,则绳子的拉力为6N.故B正确.小球转第三个半圈的时间t″=![]() =
=![]() t=4s,则t=14s时,小球转动的半径r=
t=4s,则t=14s时,小球转动的半径r=![]() l,根据F=m
l,根据F=m![]() ,则拉力变为原来的
,则拉力变为原来的![]() 倍,大小为7.5N.故C错误.细绳每跟钉子碰撞一次,转动半圈的时间少
倍,大小为7.5N.故C错误.细绳每跟钉子碰撞一次,转动半圈的时间少
![]() t=1s,则细绳第三次碰钉子到第四次碰钉子的时间间隔△t═6 3×1=3s.故D正确.故选ABD
t=1s,则细绳第三次碰钉子到第四次碰钉子的时间间隔△t═6 3×1=3s.故D正确.故选ABD
考点:圆周运动的规律;向心力。



 (当时
(当时 ,绳子对球产生拉力)
,绳子对球产生拉力) (实际上小球还没有到最高点时,就脱离了轨道)
(实际上小球还没有到最高点时,就脱离了轨道)
 (N为支持力)
(N为支持力) ,有
,有 (N为支持力)
(N为支持力) ,有
,有 (N=0)
(N=0) ,有
,有 (N为拉力)
(N为拉力)