把质量是0.2kg的小球放在竖立的弹簧上,并把小球往下按至A位置,如图甲所示;迅速松手后,弹簧把小球弹起,升至最高位置C,如图丙所示;途中经过位置B时弹簧正好处于自由状态,如图乙所示;已知B、A的高度差为0.1m,C、B的高度差为0.2m,弹簧的质量和空气阻力均忽略不计,取![]() 。
。
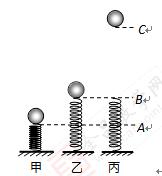
⑴求图甲状态时弹簧的弹性势能;
⑵求小球经过B点时的速度;
答案
【知识点】功能关系;弹性势能.E6
【答案解析】(1)0.6J(2)2m/s 解析: :(1)对于弹簧和小球组成的系统,小球从A→C过程,根据系统的机械能守恒得:EP=mg(hAB+hBC)=0.2×10×(0.1+0.2)J=0.6J
(2)设小球经过B点时的速度为v.小球从B→C过程,根据系统的机械能守恒得:![]() mv2=mghBC,得:v=
mv2=mghBC,得:v=![]() =2m/s
=2m/s
【思路点拨】(1)小球从A运动到C位置的过程中,对于弹簧和小球组成的系统,只有重力和弹簧的弹力做功,系统的机械能守恒,根据机械能守恒定律求解.(2)小球从B运动到C位置的过程中,只有重力做功,其机械能守恒,即可根据机械能守恒定律求解.解决本题的关键掌握机械能守恒的条件,在只有重力或弹簧弹力做功的情形下,系统机械能守恒.并能通过分析受力情况,判断小球的运动情况.


 满足
满足 时,物体可在轨道上速度减小到零,即动能可全部转化为重力势能;在
时,物体可在轨道上速度减小到零,即动能可全部转化为重力势能;在 ,物体上升到圆周最高点时的速度
,物体上升到圆周最高点时的速度 )时,物体可做完整的圆周运动;若在
)时,物体可做完整的圆周运动;若在 时,物体将在与圆心等高的位置与圆周最高点之间某处脱离轨道,之后物体做斜上抛运动,到达最高点时速度不为零,动能不能全部转化为重力势能,物体实际上升的高度
时,物体将在与圆心等高的位置与圆周最高点之间某处脱离轨道,之后物体做斜上抛运动,到达最高点时速度不为零,动能不能全部转化为重力势能,物体实际上升的高度 满足
满足 。故在解决这类问题时不能单从能量守恒的角度来考虑。
。故在解决这类问题时不能单从能量守恒的角度来考虑。