如图所示，一辆货车通过光滑轻质定滑轮提升一箱货物，货箱质量为M，货物质量为m，货车以速度v向左匀速运动，将货物提升高度h，则（　　）

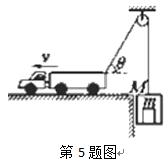
A．货物向上做匀速运动

B．箱中的物体对箱底的压力小于mg

C．图示位置时货车拉力的功率大于（M+m）gvcosθ

D．此过程中货车拉力做的功为（M+m）gh

答案

【知识点】功的计算；运动的合成和分解．D1 E1

【答案解析】C 解析：将货车的速度进行正交分解，如图所示：

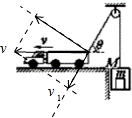
由于绳子不可伸长，货箱和货物整体向上运动的速度和货车速度沿着绳子方向的分量相等，故：v1=vcosθ由于θ不断减小，故货箱和货物整体向上做加速运动，加速度向上；A、货箱和货物整体向上做加速运动，故A错误；B、货箱和货物整体向上做加速运动，加速度向上，是超重，故箱中的物体对箱底的压力大于mg，故B错误；C、货箱和货物整体向上做加速运动，故拉力大于（M+m）g，整体的速度为vcosθ，故拉力功率P=Fv＞（M+m）gvcosθ，故C正确；D、此过程中货车拉力做的功等于货箱和货物整体动能的增加量和重力势能的增加量，大于（M+m）gh，故D错误；故选：C．

【思路点拨】由于绳子不可伸长，货箱和货物整体向上运动的速度和货车速度沿着绳子方向的分量相等，根据平行四边形定则求解出货箱和货物整体向上运动的速度表达式进行分析即可．本题关键先推导出货箱和货物整体的速度表达式，确定货箱和货物整体的运动规律，然后结合功率表达式P=Fv和动能定理列式分析，不难