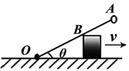
如右图所示,一根长为l的轻杆OA,O端用铰链固定,另一端固定着一个小球A,轻杆靠在一个高为h的物块上。若物块与地面摩擦不计,则当物块以速度v向右运动至杆与水平方向夹角为θ时,物块与轻杆的接触点为B,下列说法正确的是
( )
A.A、B的线速度相同
B.A、B的角速度不相同
C.轻杆转动的角速度为![]()
D.小球A的线速度大小为![]()
答案
【命题立意】本题考查圆周运动、牵连物体的速度关系。
【思路点拨】解答本题从以下几个方面考虑:(1)B点速度的分解;(2)A、B角速度相同,线速度之比等于半径之比。
【答案】C【解析】同轴转动,角速度相同,选项B错误。设图示时刻杆转动的角速度为ω。对于B点有![]() 。而A、B两点角速度相同,则有
。而A、B两点角速度相同,则有![]() ,联立解得
,联立解得![]() ,故选项C正确。
,故选项C正确。



 (当时
(当时 ,绳子对球产生拉力)
,绳子对球产生拉力) (实际上小球还没有到最高点时,就脱离了轨道)
(实际上小球还没有到最高点时,就脱离了轨道)
 (N为支持力)
(N为支持力) ,有
,有 (N为支持力)
(N为支持力) ,有
,有 (N=0)
(N=0) ,有
,有 (N为拉力)
(N为拉力)