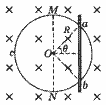
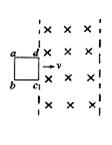
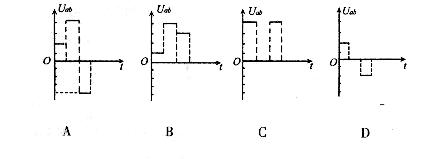
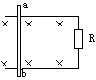
如图，一个边长为l的正方形虚线框内有垂直于纸面向里的匀强磁场；一个边长也为l的正方形导线框所在平面与磁场方向垂直；虚线框对角线ab与导线框的一条边垂直，ba的延长线平分导线框．在t＝0时，使导线框从图示位置开始以恒定速度沿ab方向移动，直到整个导线框离开磁场区域．以i表示导线框中感应电流的强度，取逆时针方向为正．下列表示i－t关系的图示中，可能正确的是( )
答案：C
解析：由题意知，当正方形导线框位移0≤x≤
时，感应电动势为E＝B·2xv＝2Bxv，而电流i＝
，i与x成正比，A错．
当≤x≤l时，E＝Blv保持不变，B错．当l<x≤(
－1)l时，两边同时切割磁感线产生电动势相互抵消，电流逐渐减小，当右边出磁场即x>l时，E迅速减小，此两段电流变化应有不同，故D错C对．
法拉第电磁感应定律：
（n为线圈匝数）。 
； 
。 导体切割磁感线的两个特例：
的区别与联系及选用原则：
电磁感应中动力学问题的解法：
电磁感应和力学问题的综合，其联系的桥梁是磁场对感应电流的安培力，因为感应电流与导体运动的加速度有相互制约的关系。
1．分析思路
(1)用法拉第电磁感应定律和楞次定律求感应电动势的大小和方向。
(2)求回路中的电流。
(3)分析研究导体受力情况(包含安培力，用左手定则确定其方向)。
(4)列动力学方程或平衡方程求解。
2．常见的动态分析这类问题中的导体一般不是做匀变速运动，而是经历一个动态变化过程再趋于一个稳定状态，故解这类问题时正确进行动态分析确定最终状态是解题的关键。同时也要抓好受力情况和运动情况的动态分析，研究顺序为：导体受力运动产生感应电动势一感应电流一通电导体受安培力一合外力变化一加速度变化一速度变化一周而复始地循环，循环结束时，加速度等于零．导体达到稳定运动状态。
电磁感应中的动力学临界问题：
(1)解决这类问题的关键是通过运动状态的分析，寻找过程中的临界状态，如速度、加速度求最大值或最小值的条件。
(2)基本思路：
登录并加入会员可无限制查看知识点解析
bcd
