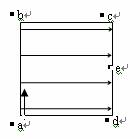
如图所示，质量相同的两个带电粒子M、N，以相同的速度沿垂直于电场方向同时射入两平行板间的匀强电场中，M从两板正中央射入，N从下极板边缘处射入，它们最后打在上极板的同一点上。不计粒子的重力，则从开始射入到打到上板的过程中 （ ）
A．它们的带电荷量之比qM: qN=1:2
B．它们在电场中的运动时间tN> tM
C．它们的电势能减少量比△EM:△EN=1:4
D．打到上极板时的速度之比为υM: υN=1:2
AC 解析：M、N运动时间相同，但加速度不同，由
，
，
, 
,解得q1:q2 =1:2。M、N电势能的减少量分别等于电场力对它们做的功
，由于q1:q2 =1：2，U1:U2=1:2所以△EM:△EN=1:4。因此A、C正确。
带电粒子在电场中的直线运动:
(1)如不计重力，电场力就是粒子所受合外力，粒子做直线运动时的要求有：
①对电场的要求：或是匀强电场，或不是匀强电场但电场的电场线有直线形状。
②对初始位置的要求：在匀强电场中任一点开始运动都可以，在非匀强电场中带电粒子的初始位置必须在直线形的电场线上。
③对初速度的要求：初速度或为零，或不为零但与所在的电场线共线。
(2)粒子在电场中做直线运动的处理方法有两种：
①将牛顿第二定律与运动学公式结合求解，这种方法只能用在匀强电场中。不考虑重力时，常用的基本方程有：
等.
②由动能定理求解不涉及时间的问题，这种方法对匀强电场、非匀强电场均适用。不考虑重力时，基本方程为：
需要特别注意的是式中U是质点运动中所经历的始末位置之间的电势差，而不一定等于题目中给定的电压，如带电粒子从电压为U的两板中点运动到某一极板上时，经历的电压仅是
1、在匀强电场中的加速问题，一般属于物体受恒力（重力一般不计）作用运动问题。处理的方法有两种：
①根据牛顿第二定律和运动学公式结合求解：
，
，
；
②根据动能定理与电场力做功，运动学公式结合求解：
。
2、在非匀强电场中的加速问题，一般属于物体受变力作用运动问题。处理的方法只能根据动能定理与电场力做功，运动学公式结合求解：
。
登录并加入会员可无限制查看知识点解析
