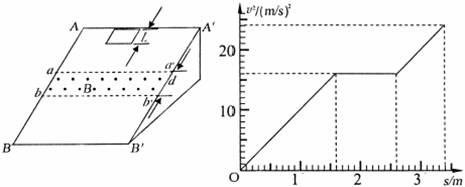
一个质量m=0.1kg的正方形金属框总电阻R=0.5Ω,金属框放在表面绝缘且光滑的斜面顶端(金属框上边与AA′重合),自静止开始沿斜面下滑,下滑过程中穿过一段边界与斜面底边BB′平行、宽度为d的匀强磁场后滑至斜面底端(金属框下边与BB′重合),设金属框在下滑过程中的速度为v,与此对应的位移为s,那么v2―s图象如图所示,已知匀强磁场方向垂直斜面向上,g=10m/s2。
(1)根据v2―s图象所提供的信息,计算出斜面倾角θ和匀强磁场宽度d.
(2)金属框从进入磁场到穿出磁场所用的时间是多少?
(3)匀强磁场的磁感应强度多大?
答案
⑴由图象可知,从s=0到s1=1.6 m过程中,金属框作匀加速运动,由公式v2=2as可得金属框的加速度为:
![]() m/s2
m/s2
根据牛顿第二定律:
mgsinθ=ma1
则:![]()
金属框下边进磁场到上边出磁场,线框做匀速运动.
故: Δs=2L=2d=2.6-1.6=1m, d=L=0.5m
⑵金属框刚进入磁场时,![]()
![]()
金属框穿过磁场所用的时间:
![]() s
s
(3)因匀速通过磁场,则:
![]()
所以磁感应强度的大小为: ![]()