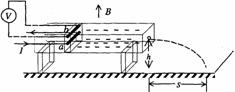
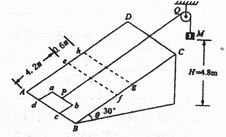
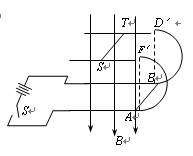
 如图所示,有上下两层水平放置的平行光滑导轨,间距是L,上层导轨上搁置一根质量为m,电阻是R的金属杆ST,下层导轨末端紧接着两根竖直平面内的半径为r的光滑绝缘半圆形轨道,在靠近半圆形轨道处搁置一根质量也是m,电阻也是R的金属杆AB。上下两层平行导轨所在区域里有一个竖直向下的匀强磁场。当闭合开关S后,当有电荷量q通过金属杆AB时,杆AB滑过下层导轨,进入半圆形轨道并且刚好能通过轨道最高点D′F′后滑上上层导轨。设上下两层导轨都是够长,电阻不计。
如图所示,有上下两层水平放置的平行光滑导轨,间距是L,上层导轨上搁置一根质量为m,电阻是R的金属杆ST,下层导轨末端紧接着两根竖直平面内的半径为r的光滑绝缘半圆形轨道,在靠近半圆形轨道处搁置一根质量也是m,电阻也是R的金属杆AB。上下两层平行导轨所在区域里有一个竖直向下的匀强磁场。当闭合开关S后,当有电荷量q通过金属杆AB时,杆AB滑过下层导轨,进入半圆形轨道并且刚好能通过轨道最高点D′F′后滑上上层导轨。设上下两层导轨都是够长,电阻不计。
⑴求磁场的磁感应强度。
⑵求金属杆AB刚滑到上层导轨瞬间,上层导轨和金属杆组成的回路中的电流。
⑶问从AB滑到上层导轨到具有最终速度这段时间里上层导轨回路中有多少能量转变为内能?
答案
解:⑴开关闭合后,有电流通过AB棒,在安培力F作用下获得加速度,离开下层
轨道时速度为v0,由动量定理,得![]() ⑴
⑴
AB棒在半圆轨上运动时,机械能守恒,则![]() ⑵
⑵
AB棒在半圆轨最高点时,由牛顿第二定律得![]() ⑶
⑶
联解⑴⑵⑶式,得:![]()
⑵AB滑入上层轨道瞬间的速度为![]() ;
;
产生感应电动势为![]()
回路中电流 ![]()
⑶当两杆速度相等时,回路中磁通量不变化,电流为零,两杆作匀速直线运
动,达到最终速度v,由动量守恒定律,得:![]()
![]()
由能量关系,得:![]()