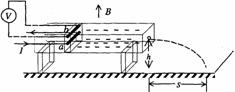
如图甲所示,空间存在B=0.5T,方向竖直向下的匀强磁场,MN,PQ是放在同一水平面内的平行长直导轨,其间距L=0.2m,R是连在导轨一端的电阻,ab是跨接在导轨上质量m=0.1的导体棒,从零时刻开始,对ab施加一个大小为F=0.45N,方向水平向左的恒定拉力,使其从静止开始沿导轨运动,此过程中棒始终保持与导轨垂直且良好接触,图乙是棒的速度一时间图象,其中AO是图象在O点的切线(切线的斜率即为棒在O点的加速度),AB是图象的渐近线。
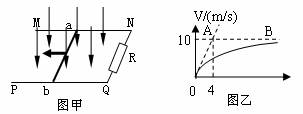
(1)除R以外,其余部分的电阻均不计,求R的阻值。
(2)当棒的位移为100m时,其速度已经达到10m/s,求此过程中电阻上产生的热量Q。
答案
解:(1)由图可知,棒在起点处的加速度![]()
由牛顿第二定律可知: ![]()
![]()
稳定后: ![]()
![]()
又∵![]()
∴ ![]()
![]()
(2)棒从静止开始到速度达10m/s的过程中,由功能关系得:
![]()
∴![]()