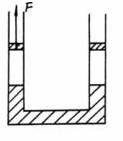
两个内径相等的容器组成一连通器，管内各有一轻质活塞，容器下部盛有足量液体，其密度为ρ，两竖直管内液面与活塞之间封闭有一定质量的气体，两管液面在同一平面上，各管内活塞与液面之间距离均为L，如图所示，现将右管内活塞用销钉固定，缓慢地提起左管内的活塞，设左管足够长，试计算两管液面高度差为L时，右管活塞因上提而移动的距离。（设管内气体开始时压强为P0，整个过程温度不变）
答案
解：右管：
左管：
左管：
两个内径相等的容器组成一连通器，管内各有一轻质活塞，容器下部盛有足量液体，其密度为ρ，两竖直管内液面与活塞之间封闭有一定质量的气体，两管液面在同一平面上，各管内活塞与液面之间距离均为L，如图所示，现将右管内活塞用销钉固定，缓慢地提起左管内的活塞，设左管足够长，试计算两管液面高度差为L时，右管活塞因上提而移动的距离。（设管内气体开始时压强为P0，整个过程温度不变）
解：右管：
左管：
左管：
查理定律:
1.概念:一定质量的某种气体，在体积不变时，压强随温度的变化叫做等容变化
2.规律:一定质量的某种气体，在体积不变的情况下，压强p与热力学温度T成正比——查理定律
3.公式:
4.推论：
5.图像: 
图线是过原点的直线，体积越大，斜率越小，即
图线是过定点
的直线，
是
的压强。
6.条件：m一定，p不太大，T不太低
7.微观解释：一定质量的理想气体，说明气体总分子数Ⅳ不变。气体体积V不变，则单位体积内的分子数不变。当气体温度升高时，分子的平均动能增大，则单位时间内跟器壁单位面积上碰撞的分子数增多，且每次碰撞器壁产生的平均冲力增大，因此气体压强p将增大
，C是比例常数或
。 登录并加入会员可无限制查看知识点解析
