如图所示,在距水平地面高h=0.80m的水平桌面一端的边缘放置一个质量m=0.80kg的木块B,桌面的另一端有一块质量M=1.0kg的木块A以初速度![]() =4.0m/s开始向着木块B滑动,经过时间t=0.80s与B发生碰撞,碰后两木块都落到地面上。木块B离开桌面后落到地面上的D点。设两木块均可以看作质点,它们的碰撞时间极短,且已知D点距桌面边缘的水平距离s=0.60m,木块A与桌面间的动摩擦因数
=4.0m/s开始向着木块B滑动,经过时间t=0.80s与B发生碰撞,碰后两木块都落到地面上。木块B离开桌面后落到地面上的D点。设两木块均可以看作质点,它们的碰撞时间极短,且已知D点距桌面边缘的水平距离s=0.60m,木块A与桌面间的动摩擦因数![]() =0.25,重力加速度取g=10m/s2。求:
=0.25,重力加速度取g=10m/s2。求:
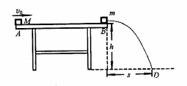
(1)两木块碰撞前瞬间,木块A的速度大小;
(2)木块B离开桌面时的速度大小;
(3)木块A落到地面上的位置与D点之间的距离。
答案
解:(1)木块A在桌面上受到滑动摩擦力f=![]() 作用做匀减速运动,根据牛顿第二定律,木块A的加速度
作用做匀减速运动,根据牛顿第二定律,木块A的加速度 ![]()
设两块木块碰撞前A的速度大小为v,根据运动学公式,得
![]()
(2)两木块离开桌面后做平抛运动,设木块B离开桌面时的速度大小为![]() ,在空中飞行的时间为
,在空中飞行的时间为![]() 。根据平抛运动规律有:
。根据平抛运动规律有:![]()
解得:![]()
(3)设两木块碰撞后木块A的速度大小为![]() ,根据动量守恒定律有:
,根据动量守恒定律有:
![]()
解得:![]()
设木块A落到地面过程的水平位移为![]() ,根据平抛运动规律,得
,根据平抛运动规律,得
![]()
则木块A落到地面上的位置与D点之间的距离![]()